VII. LES CARACTÉRISTIQUES DE LA SOCIÉTÉ LYONNAISE
Afin de dégager les caractéristiques générales de la société lyonnaise, j'ai procédé à quatre analyses factorielles des correspondances multiples (ACM) portant sur chaque coupe transversale. Dans un second temps, après avoir dégagé les grandes lignes de l'évolution, l'analyse portera sur les relations que les variables entretiennent entre elles. En effet l'analyse multivariée ne permet pas toujours, et cela est bien le cas ici, de bien dégager la nature de certaines relations et il est nécessaire de procéder à des analyses bivariées 664 . Il demeure cependant que les ACM sont les seules aptes à saisir, de manière synthétique, les tendances générales.
Les quatre analyses des correspondances multiples (ACM) utilisent exactement les quatre mêmes variables. La variable groupe professionnel comprend 12 modalités. La variable zone de résidence en comprend 15. Six classes d'âges constituent la variable âge et la variable commune de naissance regroupe 6 modalités 665 . Au total, les quatre analyses portent donc sur les quatre mêmes variables et sur trente neuf modalités (12+15+6+6). ce qui revient à dire que l'inertie des tableaux analysés est toujours la même 666 . L'intérêt de procéder de la sorte est de pouvoir vérifier si, pendant quarante ans, l'organisation des variables reste toujours la même et, si ce n'est pas le cas, d'en mesurer les variations éventuelles. C'est utiliser l'analyse factorielle, ou plus exactement une série d'analyses, comme un outil dont l'objectif n'est pas uniquement la découverte de relations mais plutôt la mesure de la permanence des relations 667 .
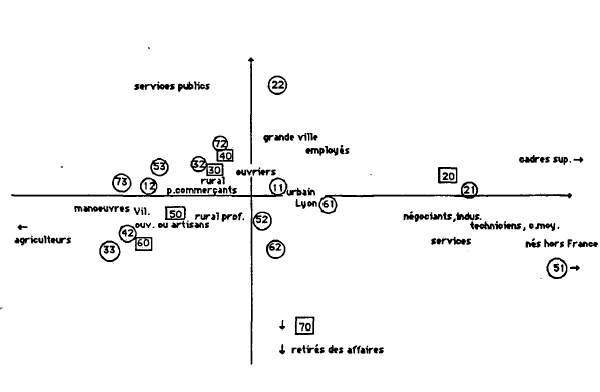
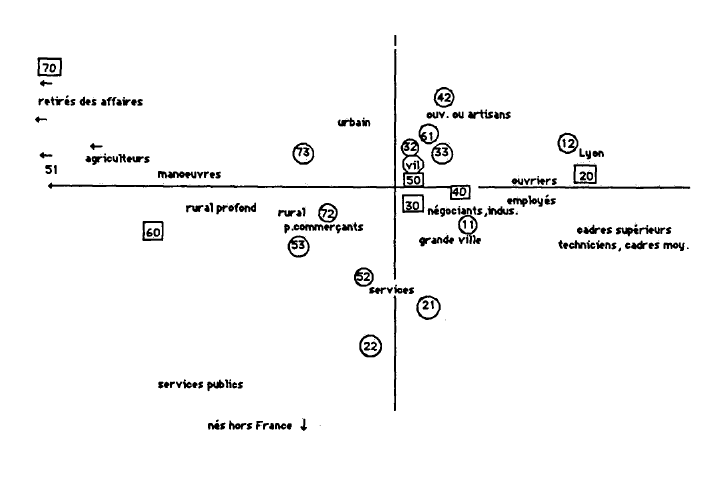
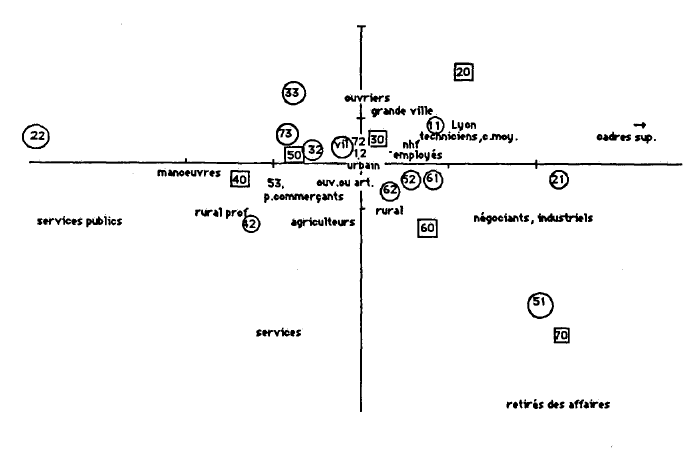
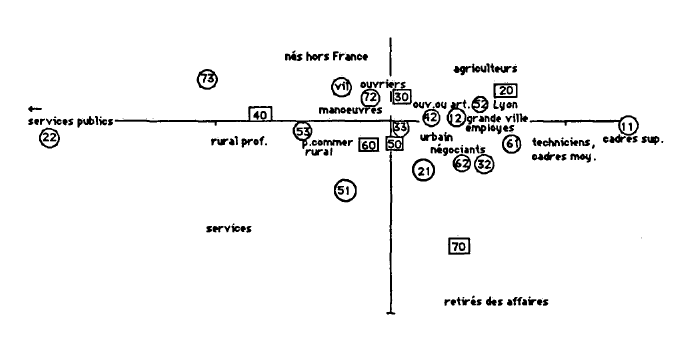
Examinons les valeurs propres, correspondant aux quatre premiers facteurs 668 des quatre analyses différentes. En cas d'indépendance des variables retenues, les trente neuf valeurs propres auraient toutes la même valeur, égale à l'inertie totale (ici 8,75) divisée par le nombre de valeurs propres (ici 39) soit 0.224 669 .
| 1896 | 1911 | 1921 | 1936 | |
| Valeur propre 1 | 0,378 | 0,391 | 0,376 | 0,369 |
| Valeur propre 2 | 0,373 | 0,362 | 0,367 | 0,354 |
| Valeur propre 3 | 0,348 | 0,346 | 0,347 | 0,318 |
| Valeur propre 4 | 0,342 | 0,341 | 0,328 | 0,308 |
Globalement les quatre séries sont comparables : les niveaux sont identiques, toujours supérieurs au niveau d'indépendance calculé ci dessus. La diminution des valeurs propres de la première à la quatrième n'est pas très rapide. Cela signifie qu'aux quatre dates, il y a une liaison entre les quatre groupes de modalités mais que cette liaison n'est pas exceptionnellement forte, ou pour le dire autrement, que chaque modalité, un groupe professionnel ou une zone de résidence par exemple, se caractérise par rapport aux modalités des autres variables par une certaine hétérogénéité. Par exemple, au sein du groupe ouvrier, certains sont nés dans des minuscules communes rurales, d'autres dans des petites villes, d'autres dans des grandes villes, d'autres à Lyon, tous n'habitent pas le même quartier et bien sûr, tous n'ont pas le même âge. La position de la modalité ouvrier tient compte de cette hétérogénéité et sa proximité avec une autre modalité ne signifie pas que les deux modalités se recoupent mais qu'il y a de grandes chances pour que la première modalité soit surreprésentée dans l'univers de la seconde, ou inversement. Par exemple, si l'on observe une nette proximité entre les hommes de 41-50 ans et la modalité rural profond (c'est à dire hommes nés dans les communes de moins de 500 habitants agglomérés au chef lieu), ce qui est le cas en 1921, cela ne signifie pas, à l'évidence, que tous les quadragénaires soient nés dans ce type de communes mais que ces deux modalités ne sont pas indépendantes. En 1921, 81 quadragénaires sont nés dans ce type de communes. Si les deux modalités étaient indépendantes, il n'y en aurait que 67. Ce que signale la proximité, c'est cette surreprésentation de 14 individus.