4.1. Les choix méthodologiques

Nous reprenons la spécification de la fonction de valorisation immobilière proposée par Yinger même si elle mesure la capitalisation intercommunale de l’offre de biens publics locaux. Nous posons comme hypothèse qu’elle peut servir dans le cadre de l’analyse de la capitalisation intracommunale. L’équation de Yinger indique notamment que le montant de la taxe foncière est complètement capitalisé dans le prix des biens immobiliers suivant l’équation (4.46) :

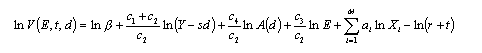
avec V la valeur vénale du bien immobilier, E les biens publics locaux, A(d) les aménités à une distance d du centre, r le taux d’actualisation, t le taux d’imposition, X_i les caractéristiques du logement, c₄/c₂ le taux marginal de substitution entre la taille du logement et le niveau d’aménités, c₃/c₂ le taux marginal de substitution entre la taille du logement et l’offre de biens publics locaux.

Les prix des logements (hors frais de notaires) de notre base de données correspondent aux prix nets des taxes foncières. Les transactions étudiées concernent des biens immobiliers localisés dans une même commune, la commune de Lyon en l’occurrence. Malgré des taxes dont le taux nominal s’applique sur tout le territoire de la commune, le niveau de la taxe foncière et la taxe d’habitation redevables par les ménages dépend de la valeur locative déterminée par les services fiscaux. Aussi, deux ménages ayant les mêmes caractéristiques et le même appartement en termes de superficie, d’équipements et de standing peuvent-ils payer des taxes différentes. Cette divergence des taxes s’explique par la localisation du logement dans la commune dont les services décentralisés du Ministère de l’économie, des Finances et de l’Industrie tiennent compte dans le calcul de la valeur locative du logement. N’ayant pas eu accès aux fichiers de l’Administration fiscale, nous posons que les impôts sont proportionnels aux prix payés par les ménages lors de la transaction (hors frais de notaires).

La méconnaissance de l’impôt payé par les ménages oblige à revoir la fonction de capitalisation. La fonction s’écrit alors de la manière suivante :

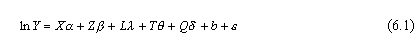
avec , , , ,  les paramètres à estimer, Y le logarithme du prix du logement net des impôts locaux (taxes foncières, taxe d’habitation), X les caractéristiques structurelles du logement, Z les caractéristiques structurelles de l’immeuble, L les variables de localisation, T les caractéristiques de l’usage et de l’aménagement de l’espace public urbain, Q les aménités, b la constante et  les résidus.

Les paramètres de la fonction des prix hédonistes seront estimés par la méthode des moindres carrées ordinaires. Plusieurs spécifications de la variable à expliquer et de la principale variable explicative principale (la superficie) ont été testées (Cf. Tableau 6.29). On observe que la spécification de la variable à expliquer sous forme logarithmique (retenu a priori) donne un coefficient de détermination le plus important avec pour variable explicative la superficie du logement sous forme logarithmique.

Tableau 6.29 : Le R² en fonction de la spécification des variables du modèle

	Spécification de la variable explicative superficie du logement
Variable à expliquer	SURF	LnSURF
PRIX	0,69	0,57
LnPRIX	0,65	0,73

Nous retenons donc les variables prix du logement et surface du logement sous leur forme logarithmique. L’introduction des autres variables a été faite progressivement en comparant le coefficient de détermination ajusté après introduction d’une variable explicative supplémentaire et le coefficient de détermination avant cette introduction et l’évolution de la valeur du Fisher. Nous avons vérifié l’ensemble par la méthode Stepwise ⁴ (pas à pas) qui permet une sélection automatique des variables explicatives en minimisant le carré des écarts entre valeur observée et valeur estimée de la variable dépendante.

L’ensemble des données exposées précédemment a été introduit dans l’équation. Les variables significatives du point de vue statistique sont rassemblées dans le tableau 6.30. Elles constituent le modèle 1.

Tableau 6.30 : Les variables de la fonction des prix hédonistes

Variable	Description	Signe attendu
Variable dépendante
LnPRIX	Prix du logement (sous forme logarithmique)
Variables indépendantes
Structure du logement
LNSURF	Superficie en m² du logement (sous forme logarithmique)	+
Structure de l'immeuble
TYPE	Variable prenant la valeur suivante en fonction de la date de construction de l’immeuble [1] avant 1948            [2] entre 1948 et 1960 [3] entre 1960 et 1980     [4] Immeuble récent	+
STAND	Variable dichotomique prenant la valeur 1 si l'immeuble a été considéré comme de standing lors de l’enquête	+
ETAGE	Variable binaire prenant la valeur 1 si le nombre d'étages est strictement supérieur à 5	+
FACADE	Variable binaire prenant la valeur 1 si la façade de l'immeuble a été renseignée comme défraîchie et très défraîchie lors de l’enquête	-
Localisation
DIST	Exponentielle négative de la distance euclidienne (en km) entre la préfecture du Rhône et le logement	+
S/P	Variable dichotomique prenant la valeur 1 lorsque l’immeuble donne sur un square ou une place	+
QUAI	Variable dichotomique prenant la valeur 1 lorsque le logement est situé sur un quai	+
Aménagement de l’espace public urbain
IBUS	Variable dichotomique prenant la valeur 1 lorsque le trafic de bus est supérieur à 500 passages par jour	-
STATBI	Variable dichotomique prenant la valeur 1 quand le stationnement devant l'immeuble est autorisé de part et d'autre de la chaussée	+
METRO	Variable binaire prenant la valeur 1 lorsque le logement se situe à moins de 150 m d’une station de métro	+
Aménités
AMEN+	Variable dichotomique prenant la valeur 1 si le niveau d'aménités de la zone environnante a été renseigné positif et très positif	+
OUVR	Pourcentage d’ouvriers dans le quartier INSEE où est localisé le logement (Recensement Général de la Population 1990)	-