4.2. L’estimation des paramètres
Le modèle 1 5 qui intègre de nombreuses variables de l’enquête réalisée, a été estimé par la méthode des moindres carrées ordinaires. Les résultats sont indiqués dans le tableau 6.31 où il ne figure que les variables significatives du point de vue statistique comme la valeur des t de Student le confirme. Tous les coefficients sont significatifs au seuil de 1 %, à l’exception de la variable distance au métro significative au seuil de 2 %, et la variable localisation sur un square ou une place significative au seuil de 5 %. Le coefficient de corrélation est relativement élevé. Les variables indépendantes retenues expliquent 78 % de la variance du prix du logement. Le sens de la relation entre la variable à expliquer et les variables explicatives est du signe attendu pour toutes les variables.
| Variables explicatives | Valeur du paramètre | Valeur du t-Student | Valeur du t-Student (hypothèse de White) |
| CONSTANTE | 8,398 | 97,67*** | 87,24*** |
| LNSURF | 1,059 | 59,04*** | 49,11*** |
| TYPE | 0,066 | 7,02*** | 7,95*** |
| STANDING | 0,071 | 3,70*** | 3,84*** |
| ETAGE | 0,079 | 3,70*** | 4,27*** |
| FACADE | -0,053 | -2,83*** | -2,77*** |
| DIST | 0,159 | 2,79*** | 2,79*** |
| S/P | 0,073 | 2,02 * | 2,34 ** |
| QUAI | 0,179 | 3,74*** | 3,40*** |
| IBUS | -0,211 | -4,03*** | -3,71*** |
| STATBI | 0,051 | 2,84*** | 2,75*** |
| METRO | 0,081 | 2,39 ** | 2,51 ** |
| AMEN+ | 0,058 | 2,92*** | 2,90*** |
| OUVR | -0,007 | -4,85*** | -4,36*** |
|
R2 : 0,782 : 0,7796 Log : -371,33 RSS : 136,379 Valeur du F : 364,27 Degré de liberté : 1322 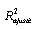 |
|||
*** significatif au seuil de 1 % ** significatif au seuil de 2 % * significatif au seuil de 5 %
L’analyse traditionnelle des résidus (projection des résidus par rapport à la variable estimée et aux variables explicatives) montre qu’il n’existe pas d’autocorrélation des résidus. En revanche, le test de Breush-Pagan montre qu’il existe de l’hétéroscédasticité. La présence d’hétéroscédasticité ne remet pas en cause l’estimation des paramètres qui demeurent non biaisés. Elle nuit à la pertinence des t de Student. En effet, les résidus de la régression sont hétéroscédastiques aussi la matrice de variance-covariance utilisée pour le calcul des t de Student ne convient plus.
White (1980) propose une nouvelle formulation de la matrice de variance-covariance afin de déterminer des t de Student moins biaisés. A la variance traditionnelle de la méthode des moindres carrés ordinaires, White substitue la formulation suivante :
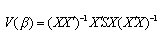
avec S la matrice diagonale des carrés des résidus de la régression.
Les résultats de l’application de l’hypothèse de White au modèle 1 figurent dans la dernière colonne du tableau 6.31. Ils confirment les résultats précédants en renforçant la significativité des résultats. Toutes les variables sont significatives au seuil de 1 %. La présence d’hétéroscédasticité dans le modèle ne remet pas en cause la pertinence des résultats présentés.
En revanche, ce premier modèle est soumis à la présence de multicolinéarité. Il existe une corrélation de certaines variables comme nous le confirme le condition number qui a une valeur de 32 (Belsley et alii.,1980). Il est généralement admis qu’à partir d’une valeur de 20 ou de 30, il faut revoir les variables explicatives du modèle (Anselin, 1998). Afin de réduire la multicolinéarité, la matrice de corrélation des variables explicatives a été étudiée afin de choisir les variables à enlever du modèle. Ce choix conduit au modèle 2 pour lequel le condition number est de 24 contre 31 avec le modèle 1. Nous nous sommes refusés à retirer d’autres variables afin de conserver l’intérêt du modèle.
L’estimation du modèle 2 figure dans le tableau 6.32. Comme pour le modèle 1, il y a présence d’hétéroscédasticité. Aussi la correction de White est-elle également indiquée dans le tableau 2. Elle confirme la significativité des paramètres au même niveau que pour le modèle 1. Le coefficient de corrélation est un peu plus faible que pour le modèle 1 (0,772 contre 0,783).
| Variables indépendantes | Valeur du paramètre | Valeur du t-Student | Valeur du t de Student (Hypothèse de White) |
| CONSTANTE | 8,435 | 102,44*** | 89,48*** |
| LNSURF | 1,078 | 60,58*** | 50,02*** |
| TYPE | 0,082 | 9,40*** | 10,19*** |
| FACADE | -0,064 | -3,52*** | -3,50*** |
| DIST | 0,151 | 2,69*** | 2,68*** |
| S/P | 0,088 | 2,44 ** | 2,77*** |
| QUAI | 0,169 | 3,62*** | 3,32*** |
| IBUS | -0,210 | -4,00*** | -3,64*** |
| STATBI | 0,060 | 3,30*** | 3,19*** |
| METRO | 0,081 | 2,36 * | 2,52 ** |
| OUVR | -0,009 | -6,30*** | -5,70*** |
|
R2 : 0,775 : 0,773 Log : -391,192 RSS : 140,495 Degré de liberté : 1325 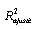 |
|||
*** significatif au seuil de 1 % ** significatif au seuil de 1,5 % * significatif au seuil de 2 %