La question des instruments mis à disposition des élèves et des étudiants dans le domaine de la statistique

Cet ensemble d’écrits constitue, en premier lieu, le versus instrumental technique de notre conception pédagogique dans sa réalisation pour l’enseignement de la statistique à des adultes étudiants en sciences de l’éducation, pour la grande majorité, non spécialistes du domaine des mathématiques et de la statistique, souvent faiblement outillés intellectuellement en mathématiques, nantis de représentations négatives à l’égard des statistiques ⁹⁶ , et à l’égard des mathématiques qu’ils reportent spontanément sur la statistique.

L’élaboration de ces instruments est le résultat de la prise en compte des interactions entre plusieurs variables d’ordre didactique, pédagogique, culturel, psychologique et institutionnel que nous essaierons d’expliciter, et de la nécessité d’une régulation du système pédagogique et didactique orienté vers l’enseignement et l’apprentissage de la statistique, instrument dominant des méthodes quantitatives.

Les conditions d’enseignement universitaire sont contraintes par la durée 12 séances de 2h sur un semestre universitaire — unité de 12 semaines — et par la taille du groupe d’étudiants d’une quarantaine à plus d’une centaine. En licence comme en maîtrise, les étudiants ont à produire une étude qui se parachève par un mémoire rédigé autour d’une problématique. Ce travail constitue une des finalités de l’enseignement des méthodes de recherche en sciences de l’éducation et des méthodes de construction, production des données, des méthodes de traitements et des méthodes de validation des hypothèses posées. Une conception de l’enseignement que nous imaginons, serait celle qui partirait des besoins émergeant dans l’étude conduite par l’étudiant pour son mémoire, accompagnée par le directeur, soit dans le cadre du GARETD (voir note 71) soit dans le cadre du séminaire de maîtrise. Les limites que nous avons repérées à une telle approche, sont celles que nous pourrions comparer à l’apprentissage sur le tas. L’étudiant ne va aborder que les concepts, les techniques et les méthodes dont il a besoin. Or une étude n’en requiert dans sa modélisation qu’un nombre restreint. Par l’ignorance des instruments dont il pourrait disposer, il risque fortement de faire des choix par défaut. C’est pourquoi nous maintenons l’option d’un enseignement de statistique comme celui d’une discipline universitaire à part entière. Nous verrons en seconde partie comment ce point de vue peut être soumis au statut que nous attribuons à la discipline.

Les conditions pédagogiques amènent à une forme dominante d’enseignement de type frontal, en cours magistral. Comment dans ces conditions, pouvons-nous organiser des séquences fondées sur les caractéristiques que nous avons évoquées plus haut à propos du tâtonnement expérimental ?

Force est de constater que les tentatives que nous avons dans le contexte même du cours, d’introduire une situation problème dont nous espérions voir se réaliser la dévolution au grand groupe, et un engager dans sa résolution se sont avérées être à minima des demi-échecs. Quand nous avons fourni une situation problème avec comme consigne un travail sur celle-ci entre deux cours, le résultat n’a pas été plus encourageant. Certes quelques étudiants s’efforçaient de respecter le contrat didactique, mais la grande majorité ne s’était nullement livrée à la confrontation avec le problème. Il ressortait un hiatus particulièrement trop important dans le grand groupe qui annulait l’efficacité espérée de la situation problème.

Ce sont ces données de réalité qui nous ont guidé vers l’élaboration d’instruments que les étudiants pourraient utiliser individuellement ou en groupe pour étudier et atteindre les objectifs que nous fixons. C’est dire que nous avons cherché à élaborer des documents qui fourniraient des situations problèmes pertinentes du point de la statistique, de celui de la méthodologie de recherche en sciences de l’éducation, dont la résolution serait ce sur quoi se fonderait le processus d’apprentissage des concepts en acceptant différents niveaux de conceptualisation. Le schéma du modèle d’enseignement pourrait être le suivant :

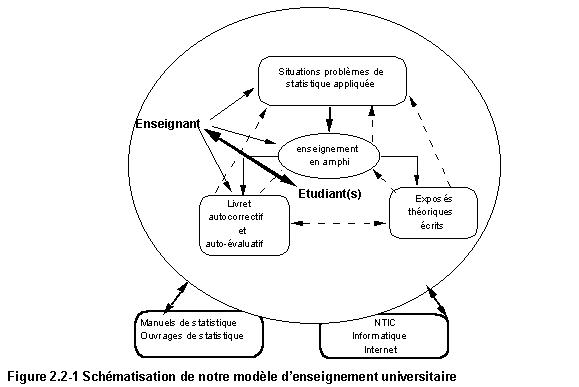
Au sens de Chevallard, nous avons procédé à une transposition didactique d’un choix de concepts, techniques et méthodes de la statistique pour les rendre enseignables. Au sens de Brousseau, ces objets et outils de la statistique sont recontextualisés dans la perspective de l’épistémologie du professeur. Au sens de Martinand, nos choix sont pilotés par des pratiques de référence comme celles mises en œuvre dans les instituts spécialisés comme l’INSEE, dans les laboratoires de recherche expérimentale, de contrôle de qualité ou dans des travaux de recherche doctorale. Comme nous le verrons dans la seconde partie, nous définissons la statistique dans la dialectique ‘« statistique mathématique ’ ‘’ ‘ statistique appliquée’». Et le pôle sur lequel nous nous arrimons, est bien celui de la statistique appliquée.

Nous avons alors bâti des situations problèmes en faisant varier divers outils statistiques et diverses configurations. Ces situations problèmes ont, pour la plupart, été confrontées à l’épreuve des faits dans la mesure où nous les avons proposées comme épreuves d’évaluation intermédiaire, type évaluation formative ou évaluation finale. De cette manière, nous avons recueilli des données importantes au travers des copies, que nous avons organisées, classées, interprétées et réinvesties dans la situation problème que nous élaborions ensuite. Nous avons organisé des séances où nous remettions les copies corrigées aux étudiants à partir desquelles nous organisions des échanges et des débats sur les erreurs ou sur les finalités même de la situation problème. C’est dans ce cadre d’échange que nous éprouvions la pertinence de nos interprétations des erreurs commises. Un cas exemplaire est apparu avec la notion de données manquantes. Dans une situation problème portant sur une étude d’une variable “nombre de réussite“ à un QCM, nous avions introduit dans la liste des individus rapportant les séries statistiques, des absents. Nombre d’étudiants ont calculé la moyenne de cette variable comme si les absents avaient obtenu le score 0. Ceci est concevable. Le problème est que leur modèle n’était pas respecté jusqu’au bout puisque le calcul de la variance ne respectait pas ce modèle. Le débat que nous avons eu, nous a fourni des éclairages pour interpréter cette particularité anodine comme un obstacle et pour en conclure que le fait de mettre des données manquantes pouvait être considéré comme une variable didactique.

1996e	Statistique et méthodes quantitatives : situations problèmes et documents autocorrectifs, cours de maîtrise de sciences de l'éducation, Lyon : ISPEF-Université Lumière, 1996, (4ème édition) 39 p.
1997i	Statistique et méthodes quantitatives : situations problèmes et documents autocorrectifs, cours de licence de sciences de l'éducation, Lyon : ISPEF-Université Lumière, 1997, (5ème édition) 80 p.

Puis pour apporter des sources théoriques complémentaires auxquelles l’étudiant peut puiser, nous avons réalisé un document d’exposés théoriques, un mixte de manuel de statistique, de répertoire de fiches techniques, de formulaire. Nous avons introduit des présentations de concepts statistiques dans des formes qui nous semblaient être plus accessibles aux étudiants ; Nous avons utilisé des données recueillies au cours des échanges soit en amphithéâtre comme nous l’avons déjà dit plus haut, soit au cours d’entretien sur un mode emprunté à l’entretien d’explicitation de Pierre Vermersch (Vermersch 1994). Les difficultés que les étudiants exprimaient, nous ont servi à construire le contenu. Toutefois, cet ouvrage dont l’acquisition est laissée au libre choix de chacun et ne s’oppose à l’usage d’aucun autre manuel, comporte aussi des documents et des informations que nous avons saisies à la source même des revues originales. De cette manière, celui-ci revêt une certaine originalité, surtout si nous lui ajoutons quelques éléments de notre propre production comme la présentation du prolongement d’une variable discrète à valeur entière à une variable continue [1996a tome 1 p. 144-149]. Nous avons construit une table [1996a tome 1 p. 122-127] donnant la distribution de la variable centrée réduite de Laplace-Gauss, pour des valeurs allant de 0 à 5 avec un pas 5/1000. Mais aussi une série de tables du Khi-deux de ddl=1 à ddl =130, [1996a tome 1 p. 113-116]. Ce qui donne à l’étudiant un outil d’une grande précision qu’il ne trouve pas habituellement. Évidemment, désormais il peut utiliser les fonctions du logiciel Excel, mais il s’agit là d’une autre voie que nous essaierons d’aborder plus tard. Nous fournissons aussi des histogrammes exactes de la variable de Pearson (dit du Khi-deux) [1996a tome 1 p. 117-119]. Sa structure reste aussi ouverte, laissant le soin à l’étudiant de poursuivre l’étude pour compléter des cas non encore exposés. En ce qui concerne la notion d’échantillonnage [1996a tome 2 p. 37-46], nous avons ouvert la liste des statistiques ⁹⁷ usuelles comme la moyenne empirique, la variance empirique, etc. Pour chaque statistique, nous avons présenté dans un tableau, les cinq paramètres “espérance“, “variance“, “écart-type“, “coefficient d’asymétrie de Fisher“, “coefficient d’aplatissement de Fisher“, selon les deux modes de tirage avec ou sans remise. Mais nous n’avons pas complété toutes les cases car nous-même n’avons pas eu la réponse au moment où nous préparions ce document.

Si tout ceci constitue un ensemble basique et banal pour un statisticien confirmé, cela n’en offre pas moins un instrument permettant aux étudiants d’accéder à différents niveaux de conceptualisation, chacun selon ses besoins ou ses désirs.

Par ailleurs, l’usage nous a fait apparaître des erreurs de modélisation de certaines présentations. Il en est ainsi pour les tests de Wilcoxon et de Mann et Whitney [1996a tome 1 p. 85-88]. dont la statistique s’appuie sur les rangs. Alors que les deux échantillons de données à ranger ne comportent pas nécessairement le même effectif, nous avions sous-estimé l’importance du signifiant ‘« le tableau’ ». Nous avons présenté les deux rangements dans un tableau à deux lignes dont le nombre de cases n’est pas nécessairement le même sur chaque ligne. Cette présentation qui ne comporte pas de difficulté pour un œil expert, s’est avérée constituer un obstacle à la compréhension et l’apprentissage de ces tests.

1996a

Méthodes quantitatives et statistique : Exposés théoriques de notions fondamentales et de formules de statistique en vue de leurs applications dans les recherches en sciences de l’éducation. Lyon : ISPEF-Université Lumière, 1996, Tome 1 – 154 p. ; Tome 2 - 46 p.

À cet ouvrage, nous avons réalisé trois documents qui tentent de répondre respectivement aux questions suivantes :

• Comment peut-on respecter strictement l’anonymat dans l’estimation d’une fréquence d’un caractère confidentiel ?
• Comment peut-on explorer les liaisons entre deux variables statistiques ?
• Quelle information apporte la nullité de la covariance ? Quel intérêt peuvent avoir une représentation graphique et le rapport de corrélation ?

Notre objectif est d’offrir des pistes qui peuvent être exploitées dans les études pour le mémoire.

1992b	Respecter l’anonymat : suggestion pour une mise en œuvre de méthodes de collectes de données respectant le secret de la réponse., la lettre du CLERSE, (17), 1992, pp 10-19
1997k	Liaisons entre deux variables statistiques : comment peut-on explorer ces liaisons ?, Licence et maîtrise de sciences de l'éducation, Lyon : ISPEF-Université Lumière, 1997, 5 p.
1997l	Indépendance de deux variables et covariance : quelle information apporte la nullité de la covariance ? Quel intérêt peuvent avoir une représentation graphique et le rapport de corrélation ?, Cours de licence et maîtrise de sciences de l'éducation, Lyon : ISPEF-Université Lumière, 1997, 7 p.

Puis viennent les livrets autocorrectifs et auto-évaluatifs. En seconde partie, nous reviendrons sur les notions d’autocorrection et d’auto-évaluation dont ces instruments constituent la forme technique. Les témoignages recueillis nous confortent dans leur efficacité et leur utilité. Force est de constater qu’à notre connaissance, il n’existe pas d’ouvrages de ce type aussi détaillés.

1994c	Statistique : documents autocorrectifs et auto-évaluatifs d'aide à l'apprentissage, livret n° 1, Lyon : APPRENDRE-Sciences de l’éducation Collection “outils de base pour la recherche en éducation”, Université Lumière, (2), 1994, 69p
1994d	Statistique : documents autocorrectifs et auto-évaluatifs d'aide à l'apprentissage, livret n° 2, Lyon : APPRENDRE-Sciences de l’éducation Collection “outils de base pour la recherche en éducation”, Université Lumière, (3), 1994, 73 p
1995a	Statistique : documents autocorrectifs et auto-évaluatifs d'aide à l'apprentissage, livret n° 3, Lyon : APPRENDRE-Sciences de l’éducation Collection “outils de base pour la recherche en éducation”, Université Lumière, (4), 1995, 63p
1995b	Statistique : documents autocorrectifs et auto-évaluatifs d'aide à l'apprentissage, livret n° 4, Lyon : APPRENDRE-Sciences de l’éducation Collection “outils de base pour la recherche en éducation”, Université Lumière, (5), 1995, 53 p