Didactique et pédagogie des mathématiques et de la statistique.
Dans notre article [1984a], nous avions déjà évoqué cette question. Notre position consistait à considérer deux champs complémentaires. Le champ de la didactique des mathématiques serait au sens de Guy Brousseau celui de ‘«l'étude des phénomènes d'enseignement qui sont spécifiques de la connaissance enseignée sans être réductible au domaine du savoir auquel elle appartient.’ 102 » Quant au champ de la pédagogie, nous écrivions qu'il ‘« engloberait des phénomènes plus généraux tels que l'organisation de la classe.’» C'est aussi, semble-t-il, le point de vue de Michel Vial quand il écrit (Vial 2000 p. 25) : ‘« Ainsi, faire travailler en groupe parce qu'un savoir précis semble le nécessiter est un choix didactique, alors que choisir le même travail de groupe pour faire que les formés communiquent et se soudent comme groupe ; (...) compte tenu du temps de formation alloué, il semble bon qu'à ce moment-là les formés travaillent ensemble et que le formateur s'efface, relève de la pédagogie. » Nous partagions aussi le point de vue de Philippe Meirieu quand il notait que : « à travers les nombreux débats qui opposent la pédagogie centrée sur l'enfant et la didactique centrée sur les savoirs, se réfractent un très vieux problème philosophique en même temps que des oppositions stériles, parce que l'apprentissage, c'est précisément la recherche, la prospection permanente dans ces deux domaines et l'effort pour les mettre en contact. Il faudrait enfin qu'on arrive à sortir de cette méthode qui consiste à penser toujours sur le mode de la variation en sens inverse’ ‘ 103 ’ ‘...»’ Point de vue complété par Guy Avanzini qui écrivait : ‘« La recherche en didactique a toute sa portée et son ampleur, mais elle ne l'atteint que prise en compte dans un ensemble plus vaste, et à condition d'accepter le facteur d'irrationalité, de fortuité, que l'approche expérimentaliste prétend en vain réduire, mais que la considération des situations réelles oblige à introduire dans la compréhension de la réussite ou de l'échec scolaire.’ ‘ 104 ’ ‘»’
Cela s'accorde avec notre conception de la didactique des mathématiques et de la statistique dans sa complexité en prenant en compte :
- la dimension philosophique : l'action de l'enseignant se réfère à un modèle pédagogique plus ou moins composite et explicite ordonné à des finalités éducatives et des valeurs,
- la dimension historico-épistémologique des connaissances mathématiques et statistiques,
- la dimension psychologique : le sujet apprenant agit selon une logique d'appropriation des connaissances, soumise aux caractéristiques affectives et cognitives individuelles. De même le sujet enseignant conduit son activité d'enseignement selon une logique empreinte de sa propre logique d'apprentissage, elle-même soumise à ses caractéristiques affectives et cognitives.
- la dimension sociale : le développement cognitif individuel se réalise dans un cadre social de communication.
Pour Jean Houssaye, la pédagogie reste (Houssaye 1993 p.13) ‘« l'enveloppement mutuel et dialectique de la théorie et de la pratique éducatives par le même personne, sur la même personne. Le pédagogue est un praticien-théoricien de l'action éducative’.» Relativement à son modèle du triangle pédagogique, il détermine la variété pédagogique à partir des processus ‘«former’», ‘«enseigner’», ‘«apprendre’» correspondant respectivement aux axes Professeur-Elèves, Professeur-Savoir et Elèves-Savoir.
Mais alors où se situe la différence entre pédagogie et didactique ?
La perspective de Jean Houssaye définit la pédagogie en s'appuyant sur une sorte de principe du tiers exclu. Il nous semble alors que la didactique s'en différencierait par une tentative de s'appuyer sur la relation ternaire Enseignant-Apprenants-Connaissance.
C'est, d'ailleurs, le point de vue de Michel Develay 105 qui fait dériver la didactique des réactions aux différentes pédagogies de la relation, du contenu ou des acquisitions dont rendent compte les trois axes cités plus haut. Et l'intrication de la pédagogie et de la didactique apparaît en ce que (Astolfi et Develay 1989 p. 9) ‘« la réflexion didactique permet...de traduire en actes pédagogiques une intention éducative.’», et fait de l'enseignant ‘« un éternel artisan de génie qui doit contextualiser les outils que lui propose la recherche en didactique en fonction des conditions de ses pratiques.’ »
Au sens de Jean Houssaye, notre pratique théorique pédagogique se situerait sur l'axe ‘«apprendre» par son rattachement à la pédagogie Freinet et au travail autonome’ ‘, en raison de « la priorité (...) donnée à la construction de méthodes et de moyens qui permettent aux élèves de se saisir directement du savoir, mais tout se fait dans un climat qui trouve sa souplesse par une relation non-figées professeur-élèves’. » (Houssaye 1993 p.23).
Pour nous, le terrain privilégié demeure la salle de classe. Tout comme Jean Houssaye immerge son triangle pédagogique dans l'institution, nous ne pouvons négliger le fait que celle-ci est institutionnellement délimitée, et que les phénomènes d'enseignement qui s'y déroulent, sont soumis à des influences extérieures. Nous avons tenté de prendre en compte l'ensemble des facteurs évoqués précédemment. Dans cette perspective, nous avions proposé une sorte de triangle pédagogico-didactique complexifié dans notre mémoire de DEA de sciences de l'éducation [1986b]. Ce modèle s'inspirait métaphoriquement d'un modèle du champ électromagnétique du physicien. Nous l'utilisons pour repérer, comprendre ou expliquer les phénomènes didactiques ou pédagogiques auxquels nous nous intéressons. Nous aborderons ce modèle dans la seconde partie. Quoi qu'il en soit nous conservons le parti pris que la didactique et la pédagogie des mathématiques et de la statistique sont, avant tout, des approches praxéologiques de l'enseignement de ces disciplines, enrichies des approches axiologique, épistémologique et téléologique. Par complémentarité, au sens donné à la situation didactique à partir de la représentation triangulaire A-S-E par Yves Chevallard, nous dirions que la pédagogie peut, elle, s'intéresser isolément aux objets constitués par l'enseignant, les élèves, le savoir ou le système d'enseignement.
Pour tenter de traduire notre conception qui repousse la dépréciation de la pédagogie considérée comme (Vial 2000 p.21) ‘« lieu de l'action qui engluerait ses acteurs ; lieu du manque de temps, de contenus, de réflexion, de formation’ » et qui renonce à une didactique palliant scientifiquement tous les défauts de la pédagogie par un choix judicieux de ses objets et de ses méthodes, nous avons construit un modèle pour guider une analyse des facteurs qui conditionneraient l'action d'enseigner les mathématiques et la statistique dans la salle de classe.
Nous reprenons les deux modèles triangulaires précédents d'investigation des champs respectifs de la pédagogie et de la didactique. Mais cette fois, nous représentons la conception pédagogique ou didactique comme le barycentre des trois pôles A-E-S affectés respectivement des coefficients positifs , , (avec + + = 1), qui pondèrent l'importance relative accordée à chacun des pôles. La temporalité est intégrable par l'intermédiaire de coefficients (t), t, t fonctions du temps définies sur des intervalles [t0 ; t1] correspondant à des découpages temporels liés aux phénomènes étudiés.
Une conception pédagogique (resp. didactique) est une position d'équilibre stable à moment donné en relation à un contexte particulier : la salle de classe, entre les trois pôles Apprenant - Savoir/Connaissance - Enseignant, pondérés par l'importance relative accordée à chacun, en tant qu'objets du champ de la pédagogie (resp. de la didactique)
Ces conceptions pédagogique et didactique déterminent l'action d'enseigner.
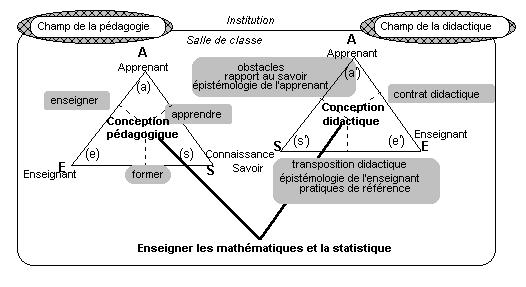
Une telle modélisation permet, en particulier, de retrouver la conception de Jean Houssaye,
comme nous l'établissons dans le tableau ci-après.
| Jean Houssaye | Triangle pédagogique (poids du pôle) |
Yves Chevallard | Triangle didactique (poids du pôle) |
||||
| axes | A (a =) | S (s=) | E (e=) | sous-systèmes | A (a' =) | S (s' =) | E (e' =) |
| «enseigner» | 0 | 1/2 | 1/2 | A-S-E | 1/3 | 1/3 | 1/3 |
| position 1 | 0 | 3/4 | 1/4 | S-E | 0 | 1/2 | 1/2 |
| position 2 | 0 | 1/4 | 3/4 | A-E | 1/2 | 0 | 1/2 |
| «former» | 1/2 | 0 | 1/2 | A-S | 1/2 | 1/2 | 0 |
| position 3 | 1/4 | 0 | 3/4 | A | 1 | 0 | 0 |
| position 4 | 3/4 | 0 | 1/4 | S | 0 | 1 | 0 |
| «apprendre» | 1/2 | 1/2 | 0 | E | 0 | 0 | 1 |
| position 5 | 3/4 | 1/4 | 0 | ||||
| position 6 | 1/4 | 3/4 | 0 | ||||
| notre conception pédagogique |
6/9 | 2/9 | 1/9 | notre conception didactique | 1/3 | 1/3 | 1/3 |
Notre conception pédagogique pourrait être caractérisée par le triplet A-E-S : (6/9, 2/9, 1/9) qui, tout en réaffirmant la part du maître, maintient une position voisine de la position 5 dans l'analyse de Jean Houssaye.
Notre conception didactique reste caractérisée par l'équipotentialité des trois pôles. En dehors de cas exprimant une contrainte simple comme la précédente, les coefficients sont donnés par leurs valeurs subjectives. Il resterait à mettre en œuvre des méthodes d'estimation de ces coefficients en fonction d'indicateurs dont Marc Bru (Bru 1991) fournit quelques pistes dans son étude des variations didactiques.
Pour achever ce propos, il serait intéressant de questionner cette modélisation par rapport au domaine de connaissance considéré : les mathématiques et la statistique. Nous pensons que par leur nature logique et épistémologique, ces disciplines se prêtent plus facilement que d'autres, à des découpages, à une désyncrétisation, à des formes de recontextualisation et de conceptualisation qui sont peut-être moins soumises aux effets de saturation par l'expérience quotidienne.
Partie 2 : Formation à et par l'autonomie des sujets apprenants dans les contextes scolaire et universitaire, en mathématiques et statistique
‘« Un des problèmes d’orientation de la recherche est celui du sort que nous devons faire aux travaux de nos prédécesseurs. Une science qui ne capitalise pas n’est pas une science. Elle reste de l’ordre de l’idéologie et de la mode. » d’après G.Vergnaud (Vergnaud 1994)’Ainsi que nous l'avons noté, l'autocorrection et l'auto-évaluation dans l'enseignement des mathématiques et de la statistique constituèrent les deux principaux objets d'étude. Cependant, la reconstitution de notre itinéraire intellectuel révéla qu'en fait, il convint de les replacer dans un axe thématique fort centré sur les processus que nous avons nommés instrumentation et autonomisation du sujet apprenant dans le cadre de l'enseignement des mathématiques et de la statistique, et autour duquel s'est organisée — et s'organise encore — notre action d'enseignant. En poursuivant notre réflexion, il nous semble que ces processus qui n'ont pas été étudiés pour eux-mêmes, sont à intégrer à une autre thématique que nous nommons formation à et par l'autonomie des sujets apprenants en mathématiques et en statistique dans les contextes scolaire et universitaire. Dans la figure ci-dessous, nous avons tenté de schématiser l'articulation de ces thématiques.
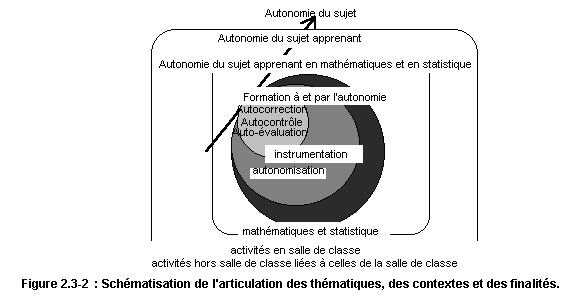
L'autocontrôle, l'autocorrection et l'auto-évaluation sont intégrés aux processus d'instrumentation et d'autonomisation au service de la formation à et par l'autonomie des apprenants. Mais du point de vue de l'enseignant, ces processus mobilisés par l'ingénierie pédagogique s'inscrivent dans des perspectives téléologique et axiologique plus larges. L'autonomie du sujet apprenant les mathématiques et la statistique par rapport à l'enseignant participe du développement l'autonomie du sujet apprenant. Et les instruments intellectuels que ce dernier acquiert ainsi, lui permettent une compréhension accrue des mondes intérieur et extérieur qui pousse vers plus d’autonomie. L'être humain est ainsi capable de plus d’autonomie en tant que membre d'une collectivité démocratique aspirant à plus de justice sociale.
Comme nous l'avons déjà abordé dans la première partie, l'autonomisation des sujets apprenants est attendue à la fois par et pour l'acquisition et l'usage d'outils conceptuels et méthodologiques des mathématiques et de la statistique. La part de l'enseignant dans la stimulation de ce processus constitua indirectement un objet d'étude, dans la mesure où une partie importante des outils pédagogiques et didactiques développés vise l'efficience de l'accompagnement et du guidage exercés par l'enseignant même. Cette considération nous amène à la rencontre de deux notions-outils dans notre perspective pédagogique, à savoir : formation et autonomie, sans pour autant les avoir étudiées comme des objets même dans nos travaux. Cette rencontre s'opéra dans le champ disciplinaire des mathématiques et de la statistique dans les contextes scolaires et universitaires. Nous avons cherché à la signifier dans le titre général de cette partie.