131. le concept d’entropie : une macro-analyse du comportement spatial

Née d’une intégrale, l’entropie est utilisée en thermodynamique pour mesurer le degré du désordre atteint par un système gazeux, mais également appliquée par les théoriciens de l’information. En thermodynamique, le principe d’entropie gouverne la dynamique de dégradation de l’énergie dans la physique des processus irréversibles loin de l’équilibre. Il décrit le parcours d’un système soumis à une excitation externe (variation de pression par exemple) qui va de l’ « ordre » au « désordre » moléculaire, c’est-à-dire d’une situation de faible probabilité à une situation de forte probabilité. On peut appliquer ce principe à l’analyse des systèmes formés d’un grand nombre d’éléments où il importe moins de connaître l’état de chaque élément particulier que le nombre d’éléments qui se trouvent dans un état particulier donné, sans tenir compte de leur individualité. Le principe d’entropie permet en effet, dans une situation d’information imparfaite, de déterminer la condition tendancielle la plus probable du système qui correspond à sa condition d’équilibre (ou d’entropie maximale).

Wilson part de la formulation d’un système spatial⁵. Celui-ci est représenté par une matrice n × m de déplacements (ou interactions) T ij entre une série de zones d’origine i , (i ∈ I, i=1..n) et de zones de destination j (j ∈ J, j=1..m). Il s’agit du cadre spatial servant de référence à l’observation générale des flux. Supposons que l’on s’intéresse aux déplacements des résidents de I vers les lieux de J pour un motif donné, le travail. T ij sont alors les déplacements domicile-travail de la population N du système, localisée en termes résidentiels en zones d’origine et en termes d’emplois en zones de destination (on suppose pour simplifier que chaque résident est un travailleur). Le tableau de contingence suivant représente une distribution du système à un moment donné.

Figure 2-. Tableau de contingence représentant une distribution du système spatial à un moment donné

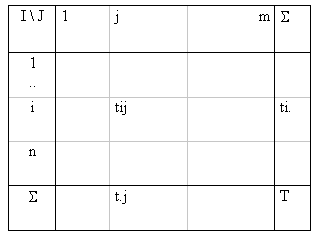
• t ij : nombre de personnes de la zone i effectuant un déplacement en j,

• t i.  : nombre de résidents de la zone i,

• t .j : nombre de personne qui se sont déplacés en j,

• T : population étudiée.

L’information de base est limitée au macro-état du système, c’est-à-dire au nombre de résidents dans chacune des zones origine O i et au nombre d’emplois dans chaque zone de destination D j tandis que le micro-état du système, c’est-à-dire la localisation de l’emploi et de la résidence de chaque individu, est inconnu, mais en réalité peu important. L’inconnue importante est le nombre d’habitants de chaque zone i qui se rend tous les jours au travail en zone j, ce que l’on peut appeler le méso-état T ij du système. La description du système spatial est quantitative et ne permet pas d’individualiser les unités statistiques qui demeurent interchangeables. Par conséquent, le nombre de fois où l’on peut obtenir cette distribution dépend des permutations pouvant être réalisées à l’intérieur des cases du tableau :

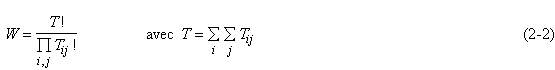
Ainsi, la distribution la plus fréquente correspond à la plus grande valeur de la fonction W. Au lieu de travailler sur cette expression complexe, Wilson considère son logarithme et introduit l’entropie du système :

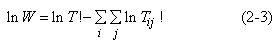
Wilson suppose que les effectifs T ij sont très importants de façon à pouvoir utiliser l’approximation de Stirling, c’est-à-dire logX! = XlogX-X.

Etant donné que ,

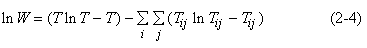
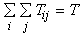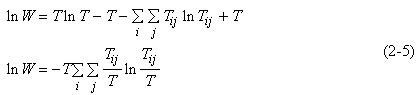
Cette dernière expression définit l’entropie du système I*J. L’entropie moyenne, notée H, est obtenue en divisant logW par T, soit :

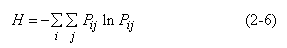
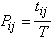où représente la probabilité qu’une personne effectue un déplacement de i vers j.

.

Comme le souligne Fustier (1988), « il faut se garder cependant d’interpréter ces probabilités comme une tentative de formalisation des comportements individuels ». Wilson ne s’intéresse pas à l’individu, sauf en tant qu’élément d’une foule dont il cherche à préciser la configuration. C’est le comportement global qui passe au premier plan de l’analyse. Pour mieux saisir la place de l’individu dans le groupe, il convient de se rappeler que l’entropie a été conçu pour mesurer le degré de désordre atteint par un système gazeux. En effet, dans l’état d’avancement des théories moléculaires, il n’est pas possible de déterminer simultanément la vitesse et la position d’une particule donnée. Mais au niveau de l’observation macroscopique, l’évolution de la configuration générale d’un système est tout à fait prévisible (entropie vient du grec qui signifie évolution). En particulier, si la quantité totale d’énergie est nulle, aucun mouvement n’est observé (l’énergie cinétique des particules est nulle), toutes les particules sont rassemblées au même endroit et l’on dit que le degré de désordre du système est à son minimum. A ce moment, l’entropie est nulle. Mais au fur et à mesure que la contrainte énergétique se desserre, c’est-à-dire lorsqu’on augmente progressivement la consommation d’énergie, les particules s’animent de mouvements individuellement désordonnés et totalement imprévisibles, mais conduisant à un degré de désordre globalement mesurable : l’entropie augmente. Lorsque l’on transpose cette analyse au système spatial, on considère que l’individu est au système spatial ce que la particule est au système gazeux : il est imprévisible sauf dans le cas particulier où l’entropie du système est nulle. En effet, si tous les déplacements ont la même origine i et le même aboutissement j, le système est parfaitement ordonné (tous les effectifs se concentrent dans la même case du tableau de contingence). Cette distribution particulière ne peut être obtenue que d’une seule manière (W=1) puisque t ij = T et t i’j’ = 0 (i’ ≠ i, et j’ ≠ j). L’entropie atteint donc sa valeur minimale pour la distribution la moins fréquente. Tout se passe comme si on obligeait une collectivité à résider au même endroit et que l’on interdise à ses éléments de se rendre ailleurs que dans un seul lieu. 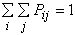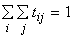En revanche si l’on diminue le poids des contraintes précédentes pour ne conserver que la seule contrainte physique , la valeur maximum de l’entropie est obtenue pour H = ln mn. Le degré de désordre le plus élevé atteint par le système spatial correspond en fait à une diffusion uniforme de l’effectif total dans chaque case du tableau. Il s’agit également de la distribution la plus fréquente. En définitive, le degré de désordre caractérisant un système spatial se trouve compris entre ces deux valeurs extrêmes, car le nombre des contraintes est moins élevé que dans le premier cas mais plus élevé que dans le second. Dans le cas d’une situation avec le maximum de contraintes (quand par exemple un planificateur territorial tout puissant décide de minimiser la consommation du sol et de maximiser les économies d’échelle dans la construction et le transport), l’habitat résidentiel et les postes de travail sont concentrés respectivement dans une seule zone : on a là une condition d’ordre maximum et de probabilité minimale. En revanche, faute de contraintes, le principe d’entropie pousse le système vers le désordre maximum et la probabilité maximum, c’est-à-dire vers une situation à répartition spatiale homogène des deux activités.