L’estimateur d’Arellano et Bond (1991)

Arellano et Bond (1991) proposent un estimateur plus efficace basé sur l’utilisation d’instruments supplémentaires, déterminant alors un ensemble de conditions sur les moments, d’où le nom d’estimation par la méthode des moments généralisé (MMG). L’estimateur d’Arellano et Bond a été très largement utilisé pour l’estimation de fonctions d’investissement sur données de panel⁶⁸ (par exemple Bond et Meghir, 1994, Jaramillo, Schiantarelli et Weiss, 1996 et Mairesse, Hall et Mulkay, 1999).

Les estimations menées par la méthode des MMG utilisent le modèle généralement transformé en terme de différences premières⁶⁹ (équation (50)).

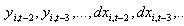Sous l’hypothèse que les erreurs νit ne sont pas autocorrélées, dνit est orthogonal aux valeurs passées de x et de y, et ainsi sont des instruments valides. Plus précisément, on peut décomposer l’équation (50) sous la forme suivante (avec t=3 correspondant à la première période où l’on observe cette relation) :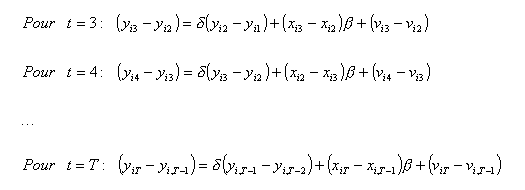

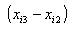Pour t=3, yil est un instrument valide pour (yi2-yi1), puisqu’ils sont fortement corrélés entre eux, et que yi1 n’est pas corrélé avec (νi3-νi2), tant que νit n’est pas autocorrélée. est lui aussi un instrument valide pour 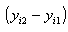, dans l’hypothèse où 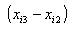est exogène. La question de l’amplitude de la corrélation avec (yi2-yi1) est d’importance même si elle est peu développée dans les études d’économétrie appliquée (Bound, Jaeger et Baker en 1995, cité par Mairesse, Hall et Mulkay, 1999). Pour t=4, les instruments possibles sont plus nombreux. En effet, on a d’une part yi2 et 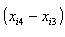qui sont valides pour les même raisons que précédemment, et d’autre part yi1 est également un instrument valide de (yi2-yi1). Enfin, pour t=T, l’ensemble des instruments possibles est 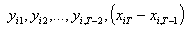. On détermine ainsi un ensemble de 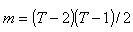restrictions linéaires sur les moments, données par 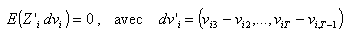et 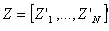la matrice des instruments, telle que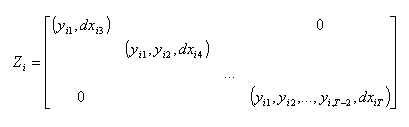

Si l’on multiplie l’équation (50) par Z’, nous obtenons sous forme matricielle:

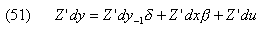
L’estimation de l’équation (51) par les MCG, fournit l’estimateur de première étape d’Arellano et Bond (1991). L’estimateur MMG en deux étapes d’Arellano et Bond (1991) est donné par:

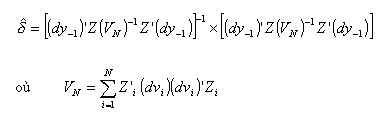
Cet estimateur MMG est consistant à la condition qu’il n’y ait pas d’autocorrélation de second ordre des différences premières des résidus. Un test de validité des instruments utilisés (et des restrictions sur les moments) peut donc être conduit à partir d’un test de cette autocorrelation d’ordre deux. Un autre test habituellement conduit pour analyser la validité des instruments utilisé est le test de Sargan (voir Hansen, 1982 et Arellano et Bond, 1991). Présentons ces deux tests.

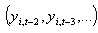L’hypothèse d’indépendance sérielle des νit est essentielle pour la consistance des estimateurs MMG, qui instrumentent la variable endogène retardée yit-1 par cette même variable avec des retards plus grands . Pour tester cette hypothèse, on peut se baser sur des tests de corrélations de premier et de second ordre des résidus en différence première 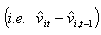. Si les résidus νit ne sont pas autocorrélés, il devrait y avoir une corrélation de premier ordre des résidus en différence première significativement négative, et pas de corrélation de second ordre de ces mêmes résidus en différence première. Ces tests sont basés sur les résidus des équations en différence première. Pour m2, sous l’hypothèse nulle d’indépendance sérielle, i.e. 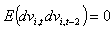, on a (Arellano et Bond, 1991):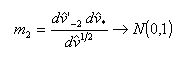

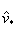correspond au vecteur 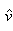, transformé de façon à ce qu’il s’accorde avec le vecteur .

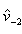Une des hypothèses nécessaires à l’utilisation d’une série d’instruments est qu’ils soient non corrélés avec le terme d’erreur, on parle alors de conditions d’orthogonalités, c’est l’hypothèse d’exogénéité. Cette hypothèse est confrontée aux données à partir d’un test de Sargan qui teste les restrictions de sur-identification. Sous l’hypothèse nulle de validité des instruments, on a:

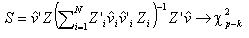
où Z est la matrice des instruments utilisés, et p le nombre de colonnes de Z.

Nous avons passé en revue trois méthodes permettant de mener des estimations économétriques sur données de panel en prenant en compte la présence de la variable endogène retardée parmi les variables explicatives. Mais, qu’en est-il du choix de l’estimateur? En fait, le choix d’une méthode particulière dépend des propriétés supposées du modèle. Comme le notent Sevestre et Trognon (1992), quatre questions sont importantes: y a-t-il des effets spécifiques individuels et/ou temporels? Ces effets spécifiques éventuels sont-ils fixes ou aléatoires? Les erreurs (non spécifiques) sont elles sphériques? Et enfin, les variables explicatives (autre que la variable endogène retardée) sont-elles parfaitement exogènes?