4.4. Formalisations mathématiques
Les objectifs de la modélisation des différents processus passés, comme dans le domaine du transport ainsi que dans d’autres domaines de l’activité humaine, s’appuient en général sur les besoins de certaines structures de mesurer les facteurs influencés le processus et d'avoir la possibilité de le simuler selon certaines modifications et de faire des pronostics. Nombreux sont des travaux consacrés à la théorie de modélisation, mais les principes sont bien présentés dans les ouvrages de A. BONNAFOUS.
Selon A. BONNAFOUS 54 trois conditions nécessaires et suffisantes doivent être respectées afin qu’un modèle puisse être qualifié de performant : à savoir la cohérence, la pertinence et la mesurabilité.
- La cohérence revêt deux aspects : la cohérence interne du discours logique, qui permet une formulation mathématique des énoncés, et la cohérence externe, qui doit permettre l’adéquation entre ce formalisme mathématique du modèle et les attributs de la réalité à appréhender (la cohérence d’objectif).
- De même, la pertinence recherchée comporte deux niveaux : il faut tendre vers la double conformité de la représentation mathématique à l’objet décrit (conformité logico-mathématique), et de la structure causale du modèle à la logique d’ensemble du phénomène réellement observé.
- La mesurabilité, enfin, qui permet à partir d’échantillons statistiques accessibles, d’estimer les paramètres et les variables retenus pour élaborer le modèle.
Deux mots sur les modèles de génération du trafic. Ils ont pour but d’étudier le trafic entre deux ou plusieurs pôles. Les formulations mathématiques de ces modèles sont plus souvent basées sur l’équation de la gravitation de Newton, évidemment avec de nombreuses autres particularités.
Les modèles de la répartition modale sont élaborés dans le but de déterminer quelles seront les parts respectives des différents modes de transport sur une liaison. Comme dans d’autres processus de modélisation, on utilise deux approches principales définies pour deux types de modèle : agrégé ou désagrégé. Nous allons davantage nous intéresser à l’examen du second type, qui s’appuie sur les observations élémentaires et les relations causales portant sur un individu. L’unité de base de ces modèles n’est pas la “ zone ”, comme dans les modèles agrégés, mais l’individu ou le ménage. On en conclue que les différentes combinaisons des aspects économiques et psychologiques joueront le rôle principal. La théorie de l’utilité est utilisée généralement dans la construction des formules de répartition modale. Mais l’utilité n’est pas toujours déterministe : des aléas interviennent résultant d’incertitudes diverses, d’une certaine instabilité des goûts. Ce sont, donc, des probabilités de choix modélisés ; l’observation des choix réels et la révélation des préférences permettent de déterminer les paramètres intervenant dans les fonctions d’utilité correspondantes. Et la répartition modale est ensuite considérée comme l’addition des choix individuels (réagrégation).
Comme l’équation algébrique on choisit généralement une distribution basée sur la loi de celle-ci logit ou de Verhulst (1845). Cette distribution peut être exprimée par les formules suivantes (par simplifications, on n’examinera que le partage modal entre deux types de transport en concurrence – une voiture particulière (VP) et des transports collectifs (TC)) :

où l’utilité U prend, dans la majorité de cas, une forme linéaire :
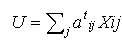
où Xij représente la j-ème caractéristique de l’alternative i à laquelle est confronté l’individu t (temps, coûts, …) ; at ij est la “ sensibilité ” de l’individu t à la caractéristique associée.
Dans certains manuels de transport cette formule est présentée comme :
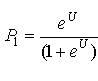
où U = a1 + a2(t1 – t2) + a3(c1 - c2), où t et c représentent le temps et le coût respectivement du premier et deuxième mode de transport.
La forme générale (avec deux variables) de la fonction de ces équations est exprimée par la formule logistique présentée comme chez SYLVESTRE-BARON 55 :
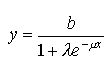
ou, pour notre cas
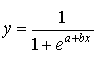
La forme canonique de cette fonction (sur le plan) est montrée dans le graphique ci-dessous :
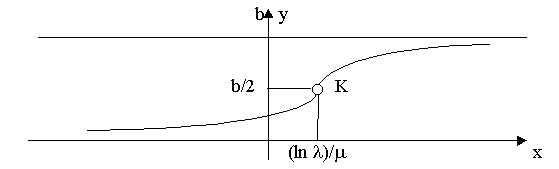
Tous ces détails sont évoqués pour des raisons de compréhension de certaines caractéristiques de cette fonction. Notamment celle de la symétrie de cette forme. Le centre de la symétrie de cette courbe est toujours, quelques soient des paramètres (les constantes λ et μ ou a et b), un point K, dont y égal à b/2 (ou, dans le cas du partage entre deux modes de transport, ½ (50 %) de la part de marché) et x est égal à (ln λ)/μ. Notamment :

Il est évident que l’existence du point de symétrie (point d’inflexion), surtout avec y qui est égal toujours à ½, limite l’application de cette forme dans certains cas, puisque, dans la situation réelle, la distribution des observations de la part de marché d’un mode de transport qui dépend même d’un seul facteur ne peut pas être symétrique dans tout l’espace envisagé. De plus, l’investigation des environs d’un point d’inflexion (ou de leur ensemble) d’une courbe asymétrique, ainsi que la position de ce point relativement aux variables examinées donnent souvent une matière à certaines conclusions.
Dans la littérature spécialisée le problème de la symétrie des formes de courbe des modèles logits est souvent présenté comme étant le plus important pour l’analyse des impacts de différents facteurs. “L’utilisation des modèles logits avec forme linéaire des variables de la fonction de l’utilité, par exemple, suppose que des gains du temps de trafic ont le même impact sur la probabilité du choix si le trajet est long ou court et applique l’existence d’une courbe symétrique dans l’espace des caractéristiques modales Xk et de l’utilité Vr. ” 56 .
Dans le même ouvrage on trouve trois possibilités pour éviter cette difficulté. La première concerne l’utilisation de modèles différents pour différents segments du marché. Cette procédure produit des approximations pièce-linéaires de la courbe véritable, mais demande beaucoup de travail. Une autre alternative peut être d'utiliser des formes non linéaires, par exemple, comme dans le cas de Box-Cox :
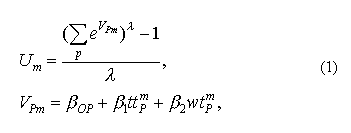
(où, par exemple, ttm p et wtm p désignent le temps de trafic et le temps d’attente associés avec la piste p par le mode m) qui, généralement, conduisent vers l’abandon des formes linéaires et supposent des solutions plus raisonnables. D’autres formes asymétriques peuvent être utilisées dans les modèles, telles que la distribution de la valeur du temps selon la loi log normal – qui applique le mode asymétrique des courbes, qui ont des formes non linéaires propres de l’utilité. On pose, donc, la principale question : “ Dépend-il la quantité de substitutions (ou complémentarités) obtenue de la courbe asymétrique de probabilité résultant des effets marginaux non constants des changements du temps de trafic, de la fréquence ou d’autres caractéristiques modales ? ” Cette équipe (les auteurs) 57 maintient l’hypothèse : “ Tous les modèles qui utilisent la distribution log normal de la valeur du temps, les transformées de Box-Cox ou la segmentation significatif ont des formes asymétriques des courbes. ”
Une autre voie peut être aussi proposée pour résoudre, du point de vue clairement mathématique, le problème de la symétrie des formes des modèles logits. Si, plus haut, il s’agissait des changements de fonctions d’utilité (de la forme linéaire à celle non linéaire) pour obtenir une asymétrie, ici nous proposons de changer la forme traditionnelle de l’équation logit. Cela donne la possibilité d’utiliser n’importe quelle formalisation mathématique pour interpréter la fonction d’utilité. Comme dans la variante précédente, ici la forme asymétrique nécessite l’intervention d’une constante (paramètre) complémentaire – un degré c. La forme générale (toujours sur le plan) de la fonction prend la forme :
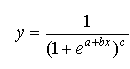
Si l’on représente la variante précédente (1) dans la forme générale, on obtient l’équation suivante (c = λ) :
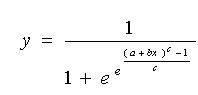
Les deux formules sont capables d’écrire théoriquement la même distribution des variables. Mais il suffit d'un coup d’œil pour constater que, du point de vue mathématique, la première formule est plus simple pour les calculs. Le degré triple de la seconde formule est remplacé par celui double dans la première. Mais il reste, dans les deux cas, le problème commun : les difficultés et surplus des efforts d’un investigateur pendant le processus de traitement des données statistiques pour obtenir les paramètres nécessaires (a, b, c) définissant les tendances de ces fonctions.
Cela est notamment le cas, quand les modèles, n’ayant pas a priori une forme linéaire, ne peuvent pas se réduire à une forme linéaire par transformation. Comme on est en présence à la fois d’opérations additive et multiplicative (dans les deux cas), il est impossible d’utiliser ici les logarithmes pour obtenir des équations normales. “ Heureusement, des ordinateurs puissants peuvent dans de tels cas toujours nous fournir des estimations MCO (moindres carrés ordinaires) et des intervalles de confiance. Une importante quantité de calculs est alors nécessaire, au lieu d’utiliser les formules simples des modèles linéaires, mais c’est de moins en moins pénible à mesure que les ordinateurs deviennent de plus en plus puissants. ” 58