Annexe 2.2.2. : L’option d’exécution différée

Un projet, dont le coût de réalisation irrécouvrable est l, est entrepris par un décideur neutre au risque. Les rendements annuels Rt sont aléatoires. Ils suivent un processus de Wiener se caractérisant par une différentielle stochastique du type :

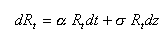
lorsque α et σ désignent les moyenne et volatilité instantanées et dz les accroissements d’un processus standard de Wiener.

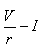Si l’investissement n’est pas rentable (Rt<l), alors le décideur désinvestit. Le coût d’opportunité subit par la firme est évalué à ARβ avec A une constante d’intégration et β une constante positive. Tant que l’investissement est rentable (Rt>l), alors il est poursuivi. Les flux de profits futurs admettent pour expression si r désigne le coût d’opportunité du capital K. Le problème du décideur est de déterminer la date optimale d’investissement lorsque la valeur du projet admet pour expression :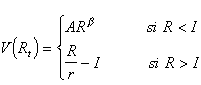

Cette approche a été généralisée aux investissements réels¹⁶¹.

Modélisation de McDonald-Siegel [1986] : Le problème du décideur consiste à élaborer une règle de décision afin de déterminer la date C*(t) à partir de laquelle il convient de s’engager de façon irréversible dans un projet. Cet investissement donne au décideur une option supposée perpétuelle qui consiste à payer des coûts irrécupérables Ft et recevoir des rendements de valeur Vt. Les coûts et les rendements sont supposés incertains.

Les coûts irrécouvrables suivent un processus de Wiener se caractérisant par une différentielle stochastique du type :

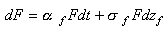
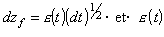où αf, σf désignent les moyenne et volatilité instantanées, dzf l’accroissement du processus de Wiener tel que une variable aléatoire non corrélée en série normalement distribuée.

Le processus de diffusion modélisant l’incertitude portant sur les rendements est considéré, dans un premier temps, comme continu puis, dans un second temps, comme discontinu c’est-à-dire modélisé sous la forme d’un processus de Poisson dq où λdésigne le taux de hasard moyen au cours d’un intervalle de temps infinitésimal et dq est tel que .

La valeur des rendements Vt est alors donnée par :

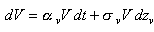• lorsque le processus de diffusion est continu,
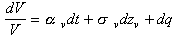• lorsque le processus de diffusion est discontinu,

lorsque αυ désigne la moyenne instantanée du processus, συ l’écart type et dzυ l’accroissement du processus de Wiener. La valeur escomptée espérée des paiements X(t) devient :

lorsque le processus de diffusion des rendements est continu :

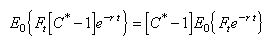
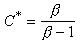où r désigne le taux de préférence pour le présent, C* la valeur seuil avec et .

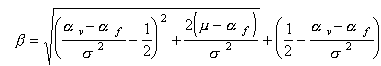lorsque le processus de diffusion des rendements est discontinu :

La nouvelle valeur de .

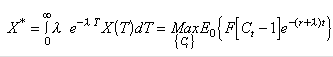
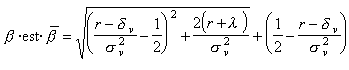Ils montrent que :

• dans la première configuration, X est une fonction croissante (resp. décroissante) des taux de volatilité 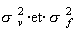(resp. du coefficient de corrélation ),

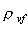• dans la seconde configuration, un accroissement du taux de hasard moyen réduit non seulement la valeur de l’option mais aussi celle de C*.

Modélisation de Pindyck [1991b] : La théorie des options réelles permet de déterminer la valeur seuil à partir de laquelle un investissement peut être entrepris. Ce cadre analytique permet également d’évaluer la valeur d’un projet V(P).

Une fois le projet entrepris, le décideur est supposé détenir un portefeuille d’options lui permettant de produire un bien au coût marginal c et de le vendre au prix aléatoire P. L’incertitude sur le prix de vente est modélisée au travers d’un processus stochastique de Wiener admettant pour expression :

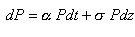
où α, σ désignent les moyenne et volatilité instantanées et dz les accroissements du processus de diffusion standard. La valeur du projet est :

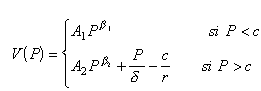
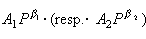Lorsque désigne le coût d’opportunité lié à l’arrêt de la production lorsque l’investissement est non rentable (resp. rentable), 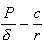la valeur présente des flux de profits futurs, δ le produit marginal lié au stockage de la production, A1 et A2 des constantes d’intégration et β1 et β2 les constantes positives.

La valeur de l’option est alors donnée par ;

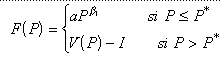
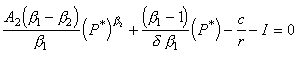avec l une somme irrécouvrable. Le prix critique P* est solution de si la valeur a est donnée par .

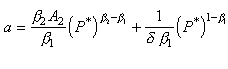Il montre que :

la valeur V(P) du projet est une fonction croissante (resp. décroissante) de la volatilité instantanée σ (resp. du coût d’opportunité du projet δ),

le prix critique est une fonction croissante de σ et de δ.

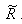Modélisation de Dixit [1992] : Attendre offre au décideur l’opportunité d’éliminer les risques les plus faibles. Soit un investissement caractérisé par des coûts K partiellement irrécouvrables et des revenus futurs aléatoires . Le coût d’opportunité de l’action immédiate est BRβ lorsque les constantes d’intégration B et positive β sont supérieures respectivement à zéro et à l’unité. La valeur du projet est donnée par :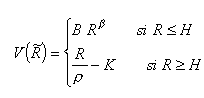

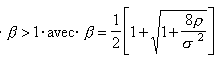où ρ supposé exogène désigne le coût d’opportunité du capital et H la valeur de l’attente. Dès lors que , l’expression de la valeur de l’attente est donnée par :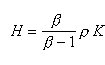

Il montre que :

• une faible incertitude engendre une faible valeur d’attente,

• si l’incertitude est forte, déterminer un seuil de décision permet d’éviter de mauvais résultats.