1.3.1. Caractéristiques empiriques générales

On aurait pu aisément préciser et amplifier notre présentation des modèles multicritères. L’échantillon présenté suffit, néanmoins, à illustrer la diversité des procédures évaluatives auxquelles le décideur est susceptible de recourir. Bien que présentant un intérêt explicatif certain, les modèles multicritères se dispensent, dans une large mesure (on l’a signalé), de précisions relatives à ce que les économistes appellent la ’fonction d’utilité’, et que les psychologues désignent, plus volontiers, sous la dénomination ’fonction de valeur’. Dans le cadre de leur ’prospect theory’, Kahneman & Tversky [1979, pp. 277-80] ont suggéré une fonction de valeur qui entend résumer un certain nombre de constats établis sur une base empirique solide. Contrairement à la pratique en vigueur au sein de la discipline économique, la fonction avancée par les auteurs assume son statut cardinal sans guère de complexes. La fonction de valeur de Kahneman/Tversky est unique à une transformation linéaire croissante près, et se voit reconnaître une portée empirique en dehors même de toute référence à des choix concernant des loteries. Outre donc sa rupture avec l’ordinalisme économique dominant, cette dernière position conduit les auteurs à rompre avec la perspective cardinaliste issue des travaux de Von Neumann & Morgenstern [1944].¹⁹¹ Ainsi, c’est avec le ’cardinalisme à l’ancienne’, celui-là qui anima les réflexions des pères fondateurs de la ’révolution marginaliste’, que renoue la fonction de valeur de Kahneman/Tversky. De façon plus spécifique, cette fonction de valeur repose sur trois caractéristiques fondamentales.

Kahneman et Tversky suggèrent, d’abord, que la valeur (ou l’utilité) est une notion éminemment relative. Elle s’avère en effet sensible à l’écart, positif ou négatif, qu’établit l’expérience considérée relativement à un ’niveau’ ou un ’point de référence’ donné (’reference point’).¹⁹² En règle générale ce point de référence est le statu quo, mais il peut également s’incarner dans un ’niveau d’aspiration’ (cf. chapitre 5, infra). Ainsi, lorsqu’il s’agit pour le décideur d’apprécier l’utilité d’une somme d’argent, celui-ci retiendra pour point de référence son niveau courant de richesse. S’il s’attend à recevoir (ou perdre) un montant particulier, alors ce niveau d’aspiration s’imposera vraisemblablement comme le point de référence pertinent. Cette première caractéristique de la fonction de valeur de Kahneman/Tversky rompt avec la perspective économique standard qui veut, en particulier, que l’utilité soit une simple fonction absolue du niveau final de richesse. Kahneman et Tversky font ensuite valoir que la fonction de valeur est généralement concave sur l’espace des gains, et convexe sur l’espace des pertes. Elle est donc concave sur l’espace des écarts positifs relativement au point de référence pertinent et convexe sur l’espace des écarts négatifs relativement à ce point.¹⁹³ Il ressort ainsi, en d’autres termes, que l’utilité ou la désutilité marginale sont décroissantes. Les auteurs remarquent, enfin, que la fonction d’utilité est plus pentue sur la région des pertes qu’elle ne l’est sur la région des gains. Cette propriété, connue sous le nom d’’aversion pour les pertes’ (’loss aversion’), traduit l’idée qu’à amplitude absolue égale, une perte est ressentie avec une plus grande intensité émotionnelle que ne l’est un gain¹⁹⁴. La fonction placée ci-dessous respecte l’ensemble de ces caractéristiques¹⁹⁵

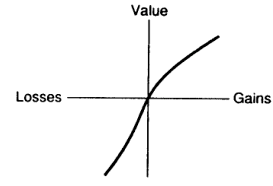
On le saisit aisément, l’analyse des processus d’évaluation et, partant, de la genèse des préférences, que suggèrent ici Kahneman et Tversky doit dépendre, dans son ensemble et de façon critique, de la localisation du point de référence (Kahneman & Tversky [1979, pp. 289-88]). Les auteurs ont, bien sûr, fait un usage abondant des propriétés de leur fonction de valeur. Ils se sont tout particulièrement attachés à rendre compte des choix en situation de risque. Pour ce faire, ils ont avancé l’existence d’une ’fonction de pondération’ visant à restituer les modalités par lesquelles le critère probabiliste vient à affecter l’évaluation des options risquées. Nous reviendrons plus loin sur ces considérations relatives à la genèse des préférences dans des contextes marqués par le risque, car il n’est pas nécessaire de quitter le domaine des conséquences déterminées, le cadre du modèle de certitude, pour faire état de la portée explicative des caractéristiques de la fonction de valeur de Kahneman/Tversky. C’est ainsi que Richard Thaler a pu mobiliser cette fonction afin de rendre compte d’une multitude de régularités empiriques qui ne manquent pas d’apparaître, au regard de l’analyse économique standard, comme autant d’’anomalies’¹⁹⁶ propres au domaine des choix en état de certitude. Présentons ici deux dimensions des travaux de l’auteur.

Notes

191.

Même si -ainsi que le signalent Kahneman & Tversky [1979, p. 280]- certains travaux ont montré, par ailleurs, que la fonction d’utilité de Von Neumann/Morgenstern (telle qu’elle a pu être inférée sur la base de choix entre des loteries) semble compatible avec les divers constats empiriques qu’entend capturer leur propre fonction de valeur.

192.

Kahneman & Tversky [1979, p. 277] suggèrent qu’il en irait en matière de jugement évaluatif, comme (ailleurs) en matière de perception. L’Homme (notamment) inscrit ses perceptions en relation à son niveau d’adaptation ou son point de référence courant, tel que défini par le contexte de ses expériences habituelles. Ils écrivent : ’Our perceptual apparatus is attuned to the evaluation of changes or differences rather than to the evaluation of absolute magnitudes’. Les jugements évaluatifs -en tant qu’ils reposeraient sur une forme de ’perception non-sensorielle’- obéiraient aux diverses lois de la perception. Aussi résulterait-il en particulier que la richesse ou, plus généralement, la valeur (ou l’utilité) soient des notions relatives, au même titre que les sensations de chaud et le froid.

193.

Là aussi, il en irait en matière de jugement évaluatif (de ’perception non-sensorielle’) comme (ailleurs) en matière de perception, puisqu’il ressort que pour un grand nombre d’aptitudes sensorielles l’homme (notamment) est davantage sensible aux variations qui interviennent au voisinage du niveau d’adaptation courant qu’aux variations de même amplitude constatées en des niveaux plus éloignés de ce niveau. Ce que Kahneman et Tversky [1979, p. 278] résument ainsi : ’Many sensory and perceptual dimensions share the propriety that the psychological response is a concave function of the magnitude of physical change’, et de pousuivre : ’We propose that this principle applies in particular to the evaluation of monetary changes’.

194.

Ainsi donc, si le point de référence de la fonction de valeur de Kahneman/Tversky, appliquée à des grandeurs monétaires, est le statu quo (i.e. le niveau de richesse présent du décideur), ces propriétés permettent d’affirmer, à titre d’exemple : a) que la plus-value (moins-value) en termes de satisfaction associée à une augmentation du niveau des gains (pertes) de 100 à 200 (de -100 à -200) est supérieure à celle qui résulte d’une progression de 1100 à 1200 (-1100 à -1200) ; b) que la satisfaction associée à un gain de 100 est inférieure (en valeur absolue) à l’insatisfaction qui résulte d’une perte de 100.

195.

Fonction de valeur de Kahneman/Tversky reproduite à partir de Thaler [1991, p.144].

196.

L’auteur a publié plusieurs articles dans le Journal of Economic Perspectives, visant tous à rendre compte d’une certaine ’anomalie’ -ce qui vaut à l’auteur une solide réputation de ’chasseur d’anomalies’. Ces articles sont repris in Thaler [1992]. Cf. Ch 2, § 1.3.2.3., supra.