1.4.1. La théorie des perspectives aléatoires de Kahneman/Tversky

De même que les modèles multicritères pourraient être, plus systématiquement, enrichis par la mise à contribution des propriétés inhérentes à la fonction de valeur de Kahneman/Tversky, de même ces modèles pourraient-ils être, plus systématiquement, raffinés en prenant acte de l’indétermination qui marque, çà et là, l’espace des conséquences. A défaut d’une telle intégration, sans doute encore prématurée, les auteurs comportementalistes paraissent tenir, avec la ’prospect theory’, une représentation qui capture, de manière empiriquement satisfaisante, certains aspects propres à la formation des jugements évaluatifs tels qu’ils se manifestent dans des contextes marqués par le risque et, plus secondairement, par l’incertitude.²⁰⁵ La théorie des perspectives aléatoires s’assigne expressément pour objectif, à l’origine, de rendre compte des modalités par lesquelles les individus intègrent le critère probabiliste aux fins de leurs choix entre diverses options risquées.²⁰⁶ En situation de risque, on suppose les probabilités données. Selon Kahneman et Tversky, néanmoins, l’information probabiliste n’affecte pas, en l’état, les préférences individuelles. Les auteurs avancent ainsi, à côté de leur fonction de valeur, l’existence d’une ’fonction de pondération’ (’weighting function’). Le décideur est censé passer au crible de cette autre fonction les probabilités dont il prend connaissance. Celles-ci se voient de la sorte transformées, leur impact sur les choix individuels s’effectuant sous cette forme modifiée.²⁰⁷

La fonction de pondération, ψ (p), capture trois constats empiriques fondamentaux. Kahneman & Tversky [1979, 1988] font ainsi valoir : 1) que les évènements impossibles sont, bien évidemment, écartés et se voient accordés une pondération nulle : ψ (0) = 0 ; que l’échelle des pondérations peut être normalisée, de sorte que l’on a : ψ (1) = 1 ; cependant, la fonction de pondération est indéterminée en ses extrémités : les pondérations effectivement retenues dans les cas de très faibles ou, au contraire, de très fortes probabilités ne peuvent être clairement anticipées²⁰⁸ ; 2) que les faibles probabilités sont sur-pondérées, alors que les probabilités de valeur intermédiaire ainsi que les fortes probabilités font l’objet, quant à elles, d’une sous-pondération ; en outre ce second effet serait plus marqué que le précédent, de sorte que l’on constate (pour p faible) : ψ (p) > p et [ψ (p) + ψ (1 - p)] < 1 (propriété dite de ’subcertitude’ ou de ’subadditivité’) ; 3) que pour un rapport de probabilités constant, le rapport des pondérations de décision associées est d’autant plus proche de l’unité que la valeur absolue des probabilités concernées est plus faible ; ainsi, à titre d’exemple, on constate (pour un rapport de 1/2) : ψ (0.1) / ψ (0.2) > ψ (0.4) / ψ (0.8) (l’ensemble de ces caractéristiques est résumé dans le schéma ci-après²⁰⁹).

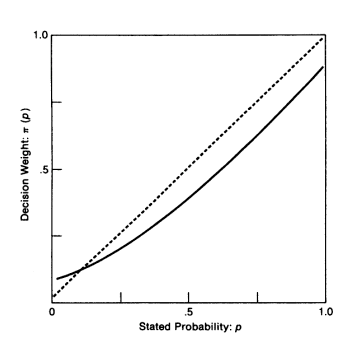
A l’instar des différents modèles de décision probabilistes, l’intégration des dimensions-critère qui renvoient, d’une part, à la valeur intrinsèque des conséquences et, d’autre part, aux croyances du décideur, s’effectue sur une base multiplicative. Kahneman & Tversky [1979] envisagent, néanmoins, deux modalités d’intégration distinctes. Le domaine de validité de ces représentations est celui des loteries simples (mettant en jeu, au plus, deux résultats non nuls), de la forme : (x, p ; y, q), pour lesquelles le décideur reçoit x avec la probabilité p, y avec la probabilité q, et 0 avec la probabilité 1 - p - q (si donc : p + q < 1). Lorsque l’on a affaire à une ’loterie standard’ (’regular prospect’) -telle que p + q < 1, ou x ≥ 0 ≥y, ou x ≤0 ≤y-, v et ψ se voient associées sur la base de l’équation qui suit :

V (x, p ; y, q) = ψ (p) v (x) + ψ (q) v (y)

Lorsque la loterie considérée est strictement positive ou strictement négative -telle, donc, que p + q = 1 et x > y > 0 ou x < y < 0-, l’équation de référence est alors la suivante :

V (x, p ; y, q) = v (y) + ψ (p) [v (x) - v(y)]

La première équation ne nécessite guère d’être explicitée. La forme particulière de la seconde équation repose, quant à elle, sur l’adhésion à l’hypothèse selon laquelle le décideur, confronté à des loteries strictement positives ou strictement négatives, dissocierait la composante certaine de la composante risquée. La composante certaine étant ’acquise’, la pondération de décision ne s’appliquerait dès lors qu’au gain ou la perte additionnel qui peut résulter pour le décideur.

Plus récemment, Tversky & Kahneman [1992] ont suggéré une extension de leur modèle originel. La ’théorie cumulative des perspectives aléatoires’ (’cumulative prospect theoey’) s’affirme comme une approche descriptive susceptible non seulement de rendre compte de la genèse des préférences en univers risqué, mais également en environnement incertain. Ainsi, dans le cadre de cette approche, les auteurs avancent que le décideur, même privé de toute information probabiliste préalable, affecte des pondérations de décision à chaque événement contingent. Par ailleurs, ces pondérations se voient désormais adossées à la ’théorie des capacités’.

Suggérée par Choquet [1954], la théorie des capacités est porteuse d’une généralisation du concept traditionnel de probabilité (objective ou subjective) qui peut donner lieu à des pondérations non-additives.²¹⁰ Surtout, la théorie permet d’édifier des pondérations de décision qui découlent, non pas de transformations une à une des probabilités sous-jacentes, mais de transformations qui mobilisent des probabilités cumulées ou des fonctions de densité. C’est ici que la théorie cumulative des perspectives aléatoires trouve, au regard de la théorie originelle, sa principale singularité analytique.²¹¹ Plus secondairement, l’originalité de la théorie cumulative des perspectives aléatoires tient au caractère dual que peut se voir conférer la fonction de pondération. Il est en effet possible de spécifier des fonctions de pondération distinctes, selon que l’on ait affaire à des gains ou à des pertes.

L’extension de la théorie originelle des perspectives aléatoires ainsi réalisée permet de rendre compte de certaines caractéristiques du choix en environnement incertain, tels que les violations de l’axiome d’indépendance rapportées par Tversky & Kahneman [1992].²¹² Elle autorise, par ailleurs, le traitement des loteries constituées d’une multitude de couples états du monde/conséquences.²¹³ Quant aux résultats établis dans le cadre de la théorie originelle, ils sont, pour l’essentiel, préservés.

Notes

205.

Cf. encadré p. 54, pour la définition ici retenue de ces concepts.

206.

Au demeurant, c’est animés de cet objectif que Daniel Kahneman et Amos Tversky se sont attachés à dégager les principales caractéristiques de la fonction de valeur individuelle présentée ci-dessus.

207.

Kahneman et Tversky [1979, p. 280] attirent cependant l’attention sur le fait que l’on a alors à faire à des ’pondérations de décision’ (’decision weights’) et non à des probabilités.

208.

D’après les auteurs, les décideurs témoigneraient généralement d’une aptitude à discriminer l’information probabiliste limitée. De la sorte, une probabilité de 0.95 sera généralement considérée soit comme renvoyant à un événement certain (et donc sur-pondérée), soit comme se référant à une réalité incertaine (mais alors, cette probabilité sera le plus souvent sous-pondérée). L’indétermination de la fonction de pondération en ses extrémités provient précisément du fait qu’il est a priori impossible de savoir à quel biais cèdera le décideur.

209.

Shéma reproduit à partir de Thaler [1991, p.141].

210.

Une capacité C est une fonction qui assigne à chaque partition A, B, de l’ensemble des états du monde S (i.e. à chaque événement), une valeur telle que C (0) = 0, C (S) = 1, et C (A) ≥C (B) si B est inclus dans A. Cette théorie peut sous-tendre des fonctions de pondération non-additives puisque, sous ces conditions -pour D et E constituant des événements mutuellement exclusifs-, C (D U E) peut être différent de C (D) + C (E) (dans le cas particulier où C s’applique à des probabilités objectives, p, q, il peut de même résulter C (p + q) différent de C (p) + C (q)). Aussi les probabilités traditionnelles apparaissent-elles comme un cas limite de la théorie des capacités, à savoir : le cas de capacités qui seraient additives.

211.

Car, il faut le rappeler, si la fonction de pondération suggérée par Kahneman & Tversky [1979] est elle-même non-additive, sa construction résulte des probabilités ’individuelles’ et non ’cumulées’ (puisque les pondérations de décision sont des transformations monotones non linéaires des probabilités associées à chaque résultat).

212.

Ainsi, d’ailleurs, que le souligne très justement la présentation de Gayant [1998], ce sont les insuffisances de l’axiome d’indépendance qui ont suscité l’essor des représentations mobilisant des pondérations de décision non-additives -représentations initialement fondées sur des transformations mettant en jeu des ’probabilités simples’ puis, plus récemment, sur des ’probabilités cumulées’.

213.

Sur un plan plus technique, une fonction de pondération dont la construction mobilise, à chaque étape, non la probabilité -objective ou subjective- associée à chaque (ensemble) de conséquence(s) en particulier, mais les probabilités cumulées ou la fonction de densité, est en mesure de fonder des préférences pour les options -risquées ou incertaines- qui respectent l’axiome de dominance stochastique du premier ordre. Ainsi, contrairement au modèle originellement suggéré par Kahneman & Tversky [1979], la théorie cumulative des perspectives aléatoires exclut qu’une option L, dont les conséquences seraient en toutes circonstances (quel que soit, donc, l’état du monde considéré) au moins aussi favorables que celles associées au choix d’une option L’, puisse ne pas être strictement préférée à L’. C’est là une concession à un impératif normatif qui peut surprendre, Tversky & Kahneman ayant montré que l’axiome de dominance est parfois violé lorsque la supériorité d’une option n’est pas évidente, ou ’transparente’.