1.2.4.1 . Principe du champ d’association

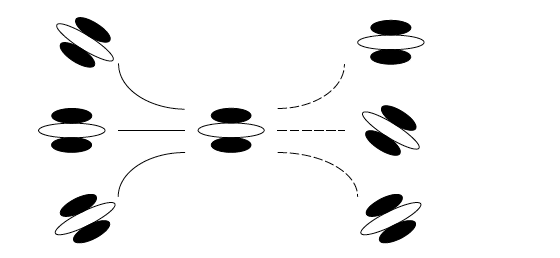
Field, Hayes et Hess (1993) ont proposé la notion de champ d’association afin d’expliquer l’intégration des contours sur des grandes régions du champ visuel. Ce concept se définit par des connexions latérales entre des cellules sensibles à la même orientation ou avec une orientation voisine. Les stimuli étaient composés de plusieurs fonctions Gabor dont l’orientation était manipulée pour être aléatoire ou, avoir la forme d’une courbe parmi d’autres signaux Gabor dont l’orientation était aléatoire. Ces deux types de stimuli étaient présentés l’un après l’autre (l’ordre de présentation était contrebalancé). La tâche des observateurs était de déterminer dans quel intervalle la courbe était présentée. Les observateurs détectaient plus facilement la cible lorsque l’orientation des signaux Gabor formant la courbe variait peu. De plus, le pourcentage de détection correcte diminuait de façon continue lorsque la différence d’orientation entre les signaux Gabor était importante. Au-delà d’une orientation de 30 deg, le pourcentage de détection était inférieur à 50%. Ce résultat est illustré dans la Figure 11 dans laquelle un lien est possible entre deux Gabor (traits pleins) ou non (traits en pointillés). Ce résultat suggère que les cellules sensibles à la même orientation ou à une orientation voisine sont connectées pour la perception des contours. Le principe du champ d’association indique que des connexions horizontales entres des neurones sensibles à des orientations voisines permettent d’intégrer des contours sur des grandes parties du champ visuel.

Figure 11 : Modèle schématique de la notion de champ d’association. Le trait continu indique que les cellules sensibles à une orientation voisine (< 30 deg) sont préférentiellement activées. L’inverse est illustré par les traits en pointillé.

Hess et Dakin (1997) ont testé si la règle du champ d’association était similaire en vision centrale et périphérique. Une courbe similaire aux précédentes était présentée en fovéa, ou à différentes excentricités. Les résultats montraient que les observateurs détectaient plus facilement la courbe apparaissant en fovéa, et que la détection diminuait quand l’excentricité augmentait jusqu’à 10 deg mais que, au-delà de 10 deg les performances ne variaient plus. Les mécanismes d’intégration de contour sont donc spécifiques de la région centrale du champ visuel. Par la suite, Hess et Dakin (1997) ont manipulé la phase des signaux Gabor (identique ou alterné), avec une présentation en fovéa ou à 20 deg d’excentricité (par rapport à un point de fixation situé dans la fovéa). Les performances diminuaient lorsque la phase était alternée et cette différence était plus importante lorsque les stimuli étaient présentés dans le champ visuel périphérique. Pour les auteurs, ce résultat indique que le champ visuel périphérique ne peut pas utiliser plus d’une opération de filtrage à la fois. On sait depuis longtemps que les fonctions visuelles dans la périphérie sont différentes de celles de la fovéa pour de nombreux aspects, et notamment l’incertitude spatiale. Hess et Dakin (1999) ont testé si ce facteur pouvait rendre compte des effets précédents. L’incertitude spatiale était manipulée dans une tâche de discrimination. Deux stimuli étaient présentés l’un après l’autre et ces stimuli étaient composés de signaux Gabor alignés, ou de signaux Gabor dont la position était incertaine le long d’un axe (selon une répartition 2D gaussienne). L’incertitude spatiale ⁸ est plus élevée dans la périphérie, donc la performance pour les Gabors « incertains » devrait être améliorée en périphérie et non pas en fovéa. Les résultats ont montré que plus le sigma de la fonction gaussienne était important (plus l’incertitude était grande) et plus la discrimination du contour se détériorait. Par ailleurs, les performances étaient toujours inférieures dans la périphérie que dans la fovéa. Ce résultat indique que l’incertitude spatiale n’a pas d’impact direct sur la réponse des observateurs. Ce facteur ne peut donc pas expliquer la diminution de performance observée dans le champ visuel périphérique. L’ensemble de ces résultats semblent donc indiquer que l’intégration des contours n’est pas possible en périphérie. Li et Gilbert (2002) ont réalisé une expérience similaire à celle de Hess et al. (1993) mais les stimuli étaient composés de segments de ligne. De plus, l’espacement entre les segments et le nombre de signaux colinéaires (la taille du contour) étaient manipulés. Les résultats indiquaient que la perception d’un contour continue diminuait lorsque l’espacement entre les segments augmentait et ce quel que soit le nombre d’éléments formant le contour. La détection des signaux colinéaires était presque nulle pour un espacement supérieur à 2 deg. Cette taille est comprise dans la zone d’interaction des connections horizontales long-range. Cette étude indique que l’intégration des éléments d’un contour est effectué pour des grandes tailles tant que l’espace entre les éléments reste en dessous d’une certaine distance.

Enfin, pour des stimuli plus complexes, Saarinen et Levi (2001) ont répliqué les résultats obtenus par Field et al. (1993) en utilisant un autre paradigme. Dans cette expérience, des éléments Gabor formaient un C et cette forme globale avaient 4 orientations différentes sur un fond gris moyen. L’observateur devait indiquer l’orientation globale de cette forme. Trois conditions étaient utilisées : dans la première condition, les segments Gabor étaient alignés avec le contour de la forme en C ; dans la seconde condition, l’orientation des segments était orthogonale à la forme ; et dans la dernière condition, les segments étaient alignés et orthogonaux. Le seuil des observateurs était plus bas dans la condition où les segments étaient alignés par rapport à la condition où les segments étaient orthogonaux. Ceci implique que des éléments locaux correctement orientés, facilitent l’identification de l’orientation d’une forme globale. Ce résultat peut être expliqué par le fait que les interactions locales permettent la diffusion d’une activité neuronale le long du contour.

En résumé, la présentation de l’ensemble de ces études a permis d’étendre les recherches de Polat et Sagi (1993, 1994) sur des grandes régions du champ visuel. D’un point de vue neurophysiologique, les connexions horizontales « long-range » permettraient d’expliquer les résultats obtenus avec la notion de champ d’association (Kovacs, 1996).