4. Nécessité de clarifier la notion de vrai en mathématiques.

Nous proposons de le faire d’abord en présentant deux tableaux qui donneront à voir les idées fortes que nous avons retenues .

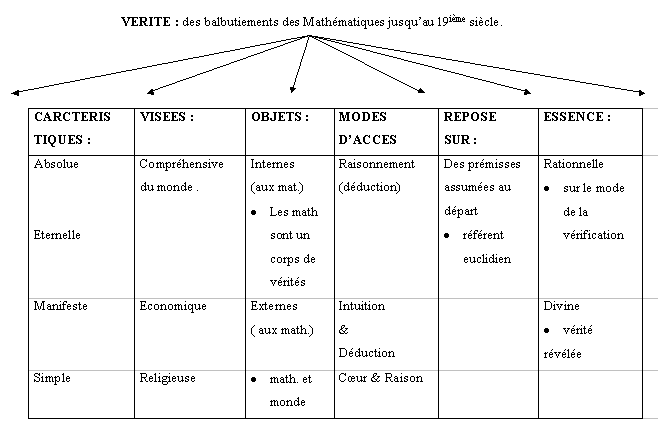
De manière à accroître leur lisibilité nous précisons le sens des titres de colonnes de ces tableaux : 

• caractéristique : ce qui a fortement imprégné l’idée du vrai.
• visée : à travers la recherche du vrai, ce à quoi aspirent les hommes.
• objet : ce sur quoi, s’applique le vrai.
• mode d’accès : le comment, on parvient à établir du vrai.
• repose sur : ce, à partir de quoi ,on peut établir du vrai.
• essence : d’où vient le vrai ?

Mise en garde pour la lecture : il n’y a aucune correspondance entre les lignes des différentes colonnes.

Pour des raisons de format nous les livrons à la page suivante.

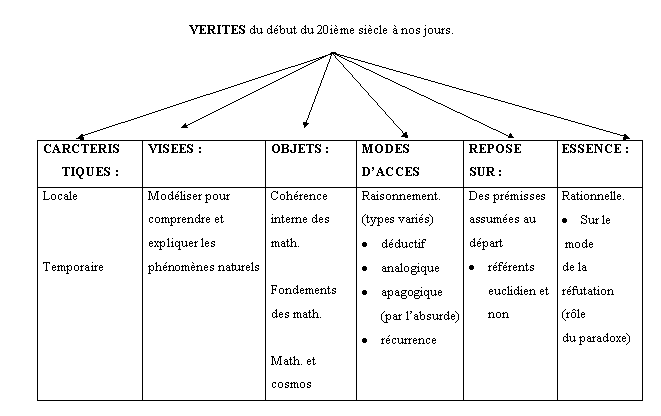
Justifions l’existence de deux tableaux et pas seulement de un.

La raison essentielle réside dans le fait de souligner qu’historiquement, il y aurait eu, comme une espèce de « rupture épistémologique », dans la manière de considérer l’idée du vrai, plus particulièrement aux abords du 20ième siècle avec la reconnaissance d’autres référents que celui d’Euclide : d’où le passage de vérité à véritéS.

C’est aussi pour souligner en conséquence, le « poids » de l’héritage grec dans l’évolution même de la notion devrai et mettre en évidence l’idée par là - même que « comme les peintres nous l’ont appris, le savoir que nous avons, bien souvent, reconstruit ce que nous voyons, fabrique nos rapprochements et notre intuition » ¹⁶⁸ .

C’est enfin pour faire émerger une idée forte qui devrait avoir un retentissement sur le plan didactico-pédagogique, à savoir, que pour que l’idée du vrai puisse être appropriée par les élèves, il serait souhaitable, de travailler chez eux la notion de doute : c’est de l’absence que naît la nécessité de présence, c’est de la lumière que jaillit l’ombre, (pensons au gnomon de Michel Serres). C’est donc en essayant d’appréhender l’idée du vrai autrement, qu’apparaîtra mieux, nous semble t-il, le sens et la visée de cette notion .

Mais il faut rappeler la mise en évidence des limites de l’idée du vrai en mathématiques, en faisant référence à trois critères fondés sur le raisonnement.

En premier lieu, le principe d’induction ne peut pas donner l’accès au vrai « nous pouvons par conséquent affirmer que les théories ne peuvent jamais être inférées des énoncés d’observation ni recevoir de ceux-ci une justification rationnelle ». ¹⁶⁹ En effet, ceci est bien connu en mathématiques car ce genre de raisonnement entraîne une régression à l’infini.

En second lieu, il faut pointer les limites du principe hypothético-déductif qui se fonde sur des prémisses assumées au départ en restant vigilant aux dérives que cette réflexion peut susciter. D’autant plus si l’on se réfère à ce que Saint Thomas D’Aquin déclarait au sujet de la science.

En vue de prouver que la théologie était une science, il rétorquait à Alexandre de Halès, maître séculier devenu franciscain et qui avançait le contraire que « les autres sciences , n’argumentent pas en vue de démontrer leurs principes, mais elles argumentent à partir d’eux pour démontrer d’autres vérités comprises dans la science. Ainsi la science sacrée ne prétend pas, au moyen de l’argumentation, prouver ses propres principes, qui sont les vérités de foi, mais elle les prend comme point d’appui, pour manifester quelque autre vérité, comme l’apôtre, dans la première épître aux corinthiens prend appui sur la résurrection du Christ pour prouver la résurrection commune ». ¹⁷⁰ Prenons la liberté dans ce texte de substituer mentalement le mot prémisses à celui de principes ; au lieu de penser science particularisons à mathématiques. Tout le problème de l’idée du vrai est parfaitement posé. Les « vérités de foi » auxquelles il est fait allusion seraient équivalentes aux axiomes d’Euclide (ou aux axiomes des autres géométries non euclidiennes). Il est aussi illusoire d’admettre que la résurrection est une prémisse incontestable que de penser que les axiomes d’Euclide sont des évidences incontestées. A la différence près, tout de même, qu’à partir de ces derniers on a pu construire une science et non un dogme (dans lesquelles les prémisses doivent être incontestées).Ce qui n’a rien du détail, puisque c’est ce qui a permis à d’autres prémisses d’émerger scientifiquement, sous entendu, en laissant libre cours à la réfutation de s’exercer. En d’autres termes, avancer quele vraien mathématiquesest contingent des prémisses de départ introduit certes, la limite du raisonnement hypothético déductif, mais ouvre la possibilité au questionnement et ne ferme pas la possibilité de les contester.

L’idée du vrai ne peut alors plus tenir en mathématiques, tel qu’elle est couramment définie dans le dictionnaire historique, c’est-à-dire comme une réalité (fin 10ième siècle) et par la suite comme la conformité de l’idée avec son objet (vers le 13ième siècle).

De plus, dans le champ des mathématiques l’histoire nous montre que cette notion  éclate, vers le 19ième siècle, avec la naissance des géométries non euclidiennes. Est-ce à dire que rien n’est vrai ou que tout l’est ? Certes pas, car ce serait dans les deux cas cautionner l’idée que les mathématiques caractérisent cet espèce de relativisation qui ouvre les portes à un dogmatisme et à un autoritarisme effrénés. Une forme de vrai existe toujours, bien sûr, mais de quelle manière ?

Au lieu de vérité, ne faudrait il pas mieux s’intéresser plus à l’idée de validité qui mettrait davantage l’accent sur le processus que le produit ? Qu’introduit ce terme de différent et pourquoi serait-il sans doute souhaitable d’y faire référence ? Parce que la vérisimilarité définie par Popper en lien avec la vérité de Tarski comme correspondance  avec les faits est un concept qui ne trouve son sens pleinement, que dans le champ des sciences empiriques. Même s’il est intéressant en mathématiques, il ne peut se justifier intégralement étant donné le problème relatif à la différence entre la nature des faits dans les deux types de sciences. Que voudrait dire qu’une proposition est plus ou moins vraie en mathématiques ? Il semblerait que ces questions soient incontournables, mais elles ne seront pas l’objet de nos préoccupations .

La stabilisation temporaire du vrai qui vient d’être présentement menée se réfère au champ scientifique. L’évolution de l’idée du vrai a été appréhendée dans le cadre du savoir de référence qui est communément appelé savoir savant,  c’est dire tout le côté spéculatif de l’entreprise.

Cependant, cette notion de vrai tient lieu de référence aussi bien dans les milieux de la doxa que dans celui de la sophia. L’idée du vrai appartient donc à tous les mondes, aussi est-ce légitime que de vouloir comprendre ce que l’on peut extraire de l’importance attribuée à cette notion.

Ni la règle, ni le principe d’universalité ne sont suffisants pour appréhender la notion de vrai : ne devrions-nous pas voir, à travers cette question du vrai une exigence plus forte qu’un simple besoin d’enseigner à prouver ? Quelle valeur transcenderait même cette possibilité de recherche/rencontre avec l’idée du vrai ? N’y aurait-il pas, derrière cette volonté de la travailler une exigence d’humanité ?

Récapitulation des idées fortes concernant l’approche épistémologique du vrai en mathématiques

• Le vrai tire sa légitimation de sa contingence avec des règles et des méthodes appartenant au champ des mathématiques
• • principes de rationalité
  • rôle des prémisses assumées au départ

• Le vrai dépend des critères que les mathématiques se donnent pour l’évaluer et des normes posées :
• • raisonnement hypothético-déductif seul valide
  • rôle du référent

• Le vrai ne dépend pas de la vérification mais de sa puissance à résister à la réfutation
• • rôle du paradoxe
  • rôle du contre-exemple