Dans le prolongement des méthodes de Poincaré

De manière assez attendue, la démarche de Poincaré s’inscrit dans le prolongement de ses études des équations différentielles et permet de renouveler l’approche des problèmes de la Mécanique céleste. Le troisième chapitre de la version corrigée du mémoire constitue le cœur du mémoire, par les techniques et les résultats qui sont exposés : la "théorie des solutions périodiques". Inspiré par le point de vue de G.W. Hill, Poincaré apporte un cortège de résultats, dont les premiers concernent l’existence de telles solutions.

Deux notions sont essentielles et directement reliées à la question de la stabilité. Les exposants caractéristiques, qui lui permettent de préciser la stabilité des solutions périodiques, et les solutions asymptotiques, définies comme étant celles qui approchent asymptotiquement les solutions périodiques instables. Poincaré parvient à démontrer l’existence de cette toute nouvelle classe de solutions et applique ces résultats dans le cas d’un système conservatif autonome.

Dans la seconde partie du mémoire, Poincaré détaille l’utilisation de ses nombreux outils mathématiques sur le problème restreint des trois corps. Pour ce système conservatif à deux degrés de liberté, Poincaré établit tout d’abord une représentation géométrique, reposant sur un système d’équations à trois variables seulement ⁸¹ . Cette vision géométrique du problème des trois corps est une des originalités du travail de Poincaré ⁸² . Il cherche ensuite à décrire le comportement des solutions asymptotiques. Dans la représentation géométrique, l’ensemble de ces solutions forme deux surfaces asymptotiques.

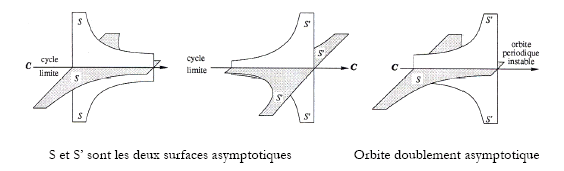
En trois étapes ⁸³ , Poincaré détermine les équations exactes des surfaces, sous forme de série. La première étape dresse une première approximation (ordre 1 dans les séries), l’objectif de la seconde étape est de fournir une approximation à un ordre quelconque, la dernière étape est le calcul de la solution exacte.