Une erreur
L’erreur commise par Poincaré est très localisée 94 .
Citons un extrait de la version corrigée du théorème :
| "Théorème III. Soit A1AMB1B une courbe invariante, de telle façon que A1 et B1 soient les conséquents de A et B. Je suppose que les arcs AA1 et BB1 soient très petits [...]. Je suppose qu’il existe un invariant intégral positif [...]. Les deux arcs AA1 et BB1 se coupent. Je me propose d’établir que c’est cette hypothèse qui est réalisée." 95 |
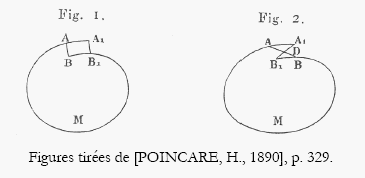
Dans la version antérieure, Poincaré avait inféré que la courbe est en fait fermée en conséquence de l’existence d’un invariant intégral.
Mais lorsqu’il corrige le problème, il découvre que l’erreur a de multiples conséquences importantes pour ses résultats, c’est ce qu’il signifie dans sa lettre à Mittag-Leffler. En effet, Poincaré avait utilisé son résultat erroné dans l’étude du comportement des solutions asymptotiques à une orbite périodique instable, sur le cas des trois corps, et avait conclu au caractère fermé des surfaces asymptotiques. Cette conclusion est remise en question et Poincaré considère désormais les orbites doublement asymptotiques, celles qui sont asymptotiques à l’orbite périodique dans le passé et dans le futur. Les invariants intégraux interviennent à nouveau pour prouver l’existence de ce type de solutions. Poincaré établit même que l’existence d’une telle solution assure l’existence d’une infinité d’entre elles.
Seconde conséquence, les conclusions relatives à la stabilité ne sont plus justifiées. Afin de ne pas laisser en suspens la question, Poincaré entame le grand remaniement du mémoire, destiné à inclure la théorie, extrêmement longue et compliquée, des orbites doublement asymptotiques.
La figure tirée du second mémoire permet de comparer les conclusions tirées par Poincaré dans les deux versions. La figure représente les traces des surfaces asymptotiques (AO’B’ et A’O’B) sur une surface de section. O’ représente la solution périodique instable générant le système de surfaces asymptotiques.

Poincaré pensait que :
• la courbe BO’B’ est fermée (i.e. B et B’ coïncident) et donc les surfaces asymptotiques sont fermées.
• ceci à des conséquences en terme de stabilité. La courbe BO’B’ délimite une surface close (et dans l’espace des phases, un volume analogue à une tore). Une solution est donc soit intérieure soit extérieure à ce volume. A une solution périodique instable correspond un système de solutions asymptotiques confinées dans une région de l’espace, et qu’on peut considérer stable à ce titre. Il pensait aussi que de telles solutions pouvaient être étudiées complètement 96 .
Dans la version corrigée, Poincaré s’interroge sur la possibilité d’avoir des surfaces asymptotiques fermées. Sur l’exemple d’un pendule simple couplé à un oscillateur linéaire il démontre qu’il n’y a en fait rien de nécessaire à cette option et constate que les courbes O’B et O’B’ peuvent se couper. Dans ce cas, une trajectoire passant par le point d’intersection appartient simultanément aux deux surfaces asymptotiques, ce qui en fait selon Poincaré, des solutions doublement asymptotiques.
Dans la première version du mémoire, Poincaré imaginait en outre que la série donnant une approximation (ordre 1) des équations des surfaces asymptotiques convergeait, alors qu’il s’aperçoit ensuite qu’elle n’est qu’une série asymptotique. La seconde étape (ordre quelconque) est donnée à titre de curiosité, en annexe, afin de compléter la description géométrique par une approche analytique : il pensait alors que ses calculs donnaient la série entière, convergente. Cette étape et la dernière étape, le calcul exact, ont fait l’objet des calculs longs et difficiles que Poincaré est obligé de réaliser en catastrophe, et montrent d’ailleurs son impressionnante dextérité en calcul.
L’erreur trouvée dans le premier mémoire est donc lourde de conséquence, plus que Poincaré ne semblait l’imaginer dans un premier temps. A côté des résultats "attendus" Poincaré révèle que la stabilité est loin d’être assurée mathématiquement dans le problème des trois corps. La résolution du problème soulève des difficultés d’une ampleur insoupçonnée.
La masse de résultats, de théorèmes et de méthodes du mémoire final va servir de base à son ouvrage le plus célèbre, les Méthodes Nouvelles de la Mécanique Céleste. Cité dans notre survol du XXème siècle, il va permettre la diffusion du travail de Poincaré (notamment en direction des astronomes) et asseoir la pertinence de son point de vue, géométrique, qualitatif. C’est dans ces pages que la notion d’orbite homocline, dont on a vu l’importance qu’il faut leur accorder, est définie comme une variante de la notion d’orbite doublement asymptotique.