a. "Period three implies chaos", 1975
Le propos de l’article est de prouver des résultats mathématiques dans le cadre des itérations du type :
x n+1 =F(x n ) (F fonction d’un intervalle dans lui-même).
Ce type d’applications a un intérêt, non seulement mathématique, mais également pour la modélisation de différents processus de la physique, de la dynamique des populations pour ne citer que quelques exemples parmi la multitude de phénomènes auxquels nous aurons à faire.
Le but est de préciser les comportements non périodiques des suites d’itérés d’un point initial x, notée : {F n (x)}. Ce comportement non périodique est justement celui qui "pourrait être appelé ‘chaotique’" 375 . Cependant, le terme chaotique est employé une seconde fois dans l’article, selon une autre "définition" : il est alors plus simplement synonyme d’irrégularité et ne correspond pas à un comportement en particulier, de type non périodique. On notera également que le titre de l’article contient le terme chaos et qu’à ce niveau il est associé à une propriété remarquable démontrée par les auteurs :
‘"Notre objectif est de comprendre les situations dans lesquelles les itérés d’un point sont très irréguliers. Un cas particulier de notre résultat principal dit que si il y a un point périodique, de période 3, alors pour tout entier n=1,2,3… il y a un point périodique de période n." 376 ’"Chaos" désigne à la fois l’"irrégularité", un comportement (une suite d’itérés) non périodique, et la propriété indiquée précédemment : posséder des points de toute période. Le terme chaos qualifie autant l’itération en tant que processus dynamique que les suites d’itérés à partir d’un point. Le titre très suggestif choisi par les auteurs cache donc en réalité un certain flou autour de ce qu’ils appellent chaos. En tout cas, en se fiant à cette seule source, il ne se dégage ni concept ni définition univoque de chaos. Pour préciser davantage, il faut retracer la genèse de l’article.
Il convient d’abord de souligner que le travail a été produit en partie en association avec le biologiste Robert May (né en 1936) 377 , un des scientifiques gravitant dans l’entourage de Li et Yorke. La lecture d’un article de May, "Biological populations with nonoverlapping generations : stable points, stable cycles, and chaos" publié en 1974, montre qu’il est très proche des positions de ceux-ci. L’article est soumis en juin 1974, publié en novembre, en vertu de quoi il devient une publication antérieure à celle de Li et Yorke évoquant le chaos. Pour être tout à fait exact, il faut également compter avec l’exposé de Li et Yorke, donné au séminaire "Dynamical systems" (du 12 au 16 août 1974) : ils brossent un rapide résumé de leur article de 1975, sous le titre "The ‘simplest’ dynamical system", et utilisent le terme "chaos" de manière plus floue qu’en 1975 378 .
La petite histoire des deux publications est racontée par Li et Yorke eux-mêmes 379 . Leur théorème était démontré dès avril 1973 et soumis à la revue American Mathematical Monthly, qui l’a rejeté car les relecteurs l’ont jugé trop obscur ; il est donc admis que ce résultat est antérieur à la publication de May mais aussi antérieur à 1975.
La rencontre avec May date de l’année universitaire 1973-74, pendant laquelle est organisé un séminaire sur le thème de la biomathématique. May, physicien reconverti à la biologie, y est invité. Celui-ci présente plusieurs résultats à propos de l’itération de la fonction logistique : Nt+1=Nt[1+r(1-Nt/K)] 380 . May s’intéresse en fait à la dynamique des populations, où cette application constitue un modèle des plus élémentaires. Il donne un résultat, inconnu de Li et Yorke, relatif au doublement de période 381 possible lorsqu’on fait varier les paramètres de la fonction logistique, tandis que May découvre les propriétés démontrées par les deux mathématiciens. Des corrections et des modifications qui ont suivies proviennent les articles de 1974 et 1975.
Le terme chaos désigne, dans l’article de May, les comportements de l’itération logistique pour lesquels on trouve soit des points périodiques de période arbitraire soit un comportement apériodique. Mais cette phrase peut laisser perplexe :
‘"Pour la biologie des populations en général, et pour les insectes des zones tempérées en particulier, l’implication est que même si le monde naturel était à 100 pour cent prédictible, la dynamique de population avec une régulation ‘dépendant de la densité’ pourrait être malgré tout, dans certaines circonstances, non distinguable du chaos, si le taux de croissance intrinsèque r était assez grand." 382 ’En croisant les analyses des différents textes, plusieurs tendances ressortent. Le terme chaos est synonyme d’irrégularité. Au fond, il y a d’abord une reprise du terme traditionnel chaos pour signifier une absence de régularité dans les itérations de certains points. Les auteurs ne précisent pas l’irrégularité en elle-même, par contre ils affirment qu’elle masque l’existence de multiples comportements périodiques et non périodiques. C’est leur résultat principal et il est d’importance : dans ces processus itératifs contraints par un mécanisme itératif (déterministe) ce chaos n’est pas une forme d’irrégularité totale ; il existe des structures périodiques affleurantes, mises en évidence par le théorème de Li et Yorke, et mélangées à des comportements non périodiques. Dès qu’une période trois est diagnostiquée, ce sont toutes les périodes qui sont présentes.
Par ailleurs, May ajoute, en 1975, un ingrédient à ce chaos, lequel deviendra prépondérant par la suite :
‘"Une autre manière de décrire le régime chaotique est d’observer que des valeurs initiales de population, proches, peuvent conduire à des trajectoires de population, avec le temps, qui divergent largement. Même si nous avons un modèle qui est très simple et complètement déterministe, en supposant tous les paramètres constants et exactement connus, le futur n’est pas prédictible. Comme souligné par Oster, les dynamiques du système sont en beaucoup d’endroits non distinguables d’un échantillon tiré d’un processus aléatoire, et sont décrites au mieux en termes stochastiques." 383 ’L’idée que le comportement dynamique imite un processus aléatoire (ou mieux : "stochastique" 384 ) n’était pas encore tout à fait explicitée dans les textes précédents, mais le choix du terme chaos renvoie directement à cette dimension aléatoire, surtout lorsqu’il est pris au sens d’irrégularité. En revanche, la "sensibilité aux conditions initiales", qui n’a pas de nom chez Li-Yorke-May encore en 1975, était complètement absente des caractérisations précédentes. Concernant ces scientifiques et à ce moment là, elle n’est qu’un aspect marginal dans leur reconnaissance du chaos. Dans ce contexte, elle est destinée à accentuer le rapprochement du mécanisme, déterministe, de l’aléatoire, conférant au terme chaos la double caractéristique d’être de l’aléatoire, au sens d’une irrégularité, à base de processus itératif, déterministe.
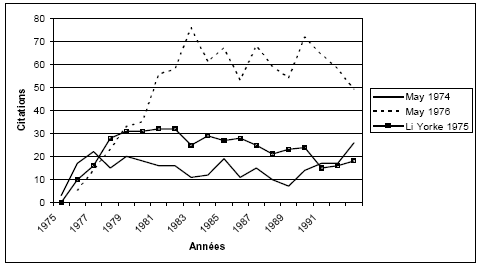
Par ses capacités à produire des textes très clairs (et des exposés sans doute aussi brillants) May est un maillon important dans la chaîne de diffusion et de publicité du chaos, tel qu’il est conçu dans l’esprit de ces trois scientifiques. L’article de May intitulé "Simple mathematical models with very complicated dynamics", publié dans Nature en 1976 constitue en quelque sorte le point d’orgue de cette série de publications. Cet article fait partie des textes les plus populaires à propos du chaos ; il est célébré et cité plus régulièrement que "Period three implies chaos", après 1980 385 :