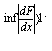L’ergodicité dans les itérations
"Period three implies chaos" est pris dans un réseau de résultats du type de la théorie ergodique des itérations, comme les réflexions de Ruelle s’inscrivent dans la problématique plus générale de la théorie ergodique des systèmes dynamiques. Les résultats de la théorie ergodique permettent à Li et Yorke de préciser les propriétés asymptotiques et statistiques des {F n (x)}, ce qui est le principal sujet de leurs investigations. Ainsi, leur dernier paragraphe est consacré aux "Propriétés statistiques de {F n (x)}".
En quelques mots, Li et Yorke procèdent à l’application de quelques théorèmes d’ergodicité sur les itérations. Pour cela "le sujet de la théorie ergodique, qui étudie des transformations sur des espaces généraux, motive la définition suivante". Il s’agit de la densité g de x, définie à partir de la fraction limite 440 φ comme :
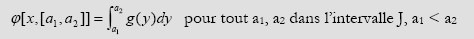
Ceci donne des indications sur la répartition asymptotique des itérés {F n (x)}. Si L(x) est l’ensemble des points limites de {F n (x)}, Li et Yorke montrent que, pour une certaine classe de fonctions 441 F, J ∞ = {y ; g(y)>0} est un intervalle et pour presque tous les x, L(x)= J ∞ . Ce résultat est publié dans un autre article des mêmes Li et Yorke : "Ergodic transformations from an interval into itself", sorti en 1978 (on aura compris que le résultat est déjà obtenu en 1975). En sus du travail de Li et Yorke, l’article de Lasota et Yorke, de 1973, encadre les considérations statistiques 442 . C’est le premier article montrant l’existence de mesures invariantes pour certaines classes d’applications F de l’intervalle [0,1], comme l’application "tente" par exemple. Ce résultat est utilisé dans la preuve du résultat présenté dans le paragraphe sur les propriétés statistiques de {F n (x)} et naturellement dans l’article de 1978.
Les résultats de Grossman et Thomae, dont nous avons tiré la précédente citation, "Le chaos a besoin d’une description probabiliste", nous permettent de mieux saisir encore le rapport entre chaos et ergodicité. C’est un article de théorie ergodique des itérations.
Leur article de 1977 repose sur les deux mêmes résultats de Lasota et Yorke (1973) et Li et Yorke (1978, obtenu en prétirage). Ils s’articulent autour des mêmes problèmes d’existence et d’unicité des densités invariantes, des fonctions de corrélations et leurs relations avec les caractéristiques des fonctions F.
Une première grande partie traite des processus ergodiques 443 , puis ils introduisent une notion de "chaos pur" : "Si, non seulement la loi dynamique, mais toutes ses itérées sont ergodiques, nous qualifions le système de purement chaotique" 444 . Ils réalisent des simulations numériques sur l’application logistique. Qualitativement, leurs résultats sont similaires aux idées de Li et Yorke : en règle général, il y a une coexistence entre des orbites périodiques et ergodiques. Leur analyse repose sur l’étude des densités invariantes et les fonctions de corrélations, des outils de la théorie ergodique permettant de préciser ces mélanges de structures. Ceci augure de "la description probabiliste du chaos".
Grossman et Thomae se donnent des méthodes pour calculer cette densité, numériquement, sur ordinateur, puis étudient le cas de l’application logistique, selon différentes valeurs du paramètre : les outils permettent d’évaluer la transition des comportements, dans l’application logistique, du périodique vers du "chaos pur". En faisant varier le paramètre a de 1 à 4, ils observent un phénomène de doublement de période, puis une valeur critique (3,5699456…) pour laquelle il y a un "chaos pur", et au-delà, des états "mixtes" (coexistence d’orbites périodiques et ergodiques). Les densités invariantes et les fonctions de corrélations permettent de visualiser et de mesurer ces superpositions de structures.