Deux exemples français : Yves Pomeau et Michel Hénon
La même année, en France, l’attracteur de Lorenz est analysé par le physicien Yves Pomeau qui réalise une série de calculs numériques avec J.L. Ibanez. L’analyse produit une sorte de complément au travail de Ruelle (et Lanford) présenté en 1975, elle en est directement inspirée 453 . Ce sont l’attracteur de Lorenz, c’est-à-dire celui correspondant aux équations différentielles originales, et sa structure géométrique qui les intéressent. Pomeau et Ibanez combinent leurs calculs numériques avec les résultats d’une analyse mathématique, reposant sur l’utilisation de sections de Poincaré. Etirement, repliement, sensibilité aux conditions initiales sont amenées naturellement dans ce contexte à propos de l’attracteur de Lorenz. On ne peut que constater la proximité des résultats de Pomeau (et Ibanez), Ruelle (et Lanford) et Rössler 454 sur ce thème de l’attracteur de Lorenz. Au passage, il faudrait remarquer que si l’analyse est finalement très mathématique, Pomeau et Ibanez suivent, en un sens, une démarche de physicien, expérimentant le système de Lorenz numériquement, grâce à un calculateur analogique 455 .
Deux ouvertures sont amenées spécifiquement par ces expériences. Elles permettent de mettre en évidence un comportement singulier du système de Lorenz : il existe une transition, caractérisée par une valeur critique des paramètres du système, pour laquelle le système bascule d’une position attracteur étrange à une configuration en cycle limite. L’importance en sera révélée par Pomeau lui-même (et un collaborateur, Paul Manneville) à travers le "scénario" de l’intermittence, proposé en 1979.
La seconde voie suggérée par Pomeau et Ibanez est l’idée de réaliser des systèmes dynamiques plus simples encore que celui de Lorenz, mais présentant des caractéristiques similaires, et qui permettraient de prouver plus clairement des "évidences" mises en lumière par les calculs numériques. Puisque le raisonnement repose sur la section de Poincaré il propose de produire une application du plan dans lui-même, plutôt qu’une équation différentielle, imitant le comportement de Lorenz et son attracteur étrange. Il en construit une de manière ad hoc qui permet de mieux fonder son raisonnement.
L’astronome Michel Hénon exploitera cette suggestion, pour obtenir un système très simple. Celui-ci est présent au séminaire de Nice (sur la turbulence), en janvier 1976 lorsque Pomeau expose justement cet aspect de ses réflexions. La familiarité de Hénon avec les applications du plan dans lui-même, lui permet de réagir rapidement et de produire un système très simple donnant un attracteur étrange 456 . Il est connu depuis sous le nom de système de Hénon 457 et correspond à l’application suivante :

où a, b sont des constantes (il aurait un attracteur étrange pour les valeurs a=1,4 et b=0,3 ; voir les figures ci-dessous).
Il est intéressant de saisir que c’est le démontage du système de Lorenz par Pomeau qui emmène Hénon vers son système. L’étirement et le repliement sont des éléments qui guident Hénon. Le choix des valeurs des paramètres est plus approximatif et c’est par tâtonnements que des valeurs adéquates de a et b sont retenues.
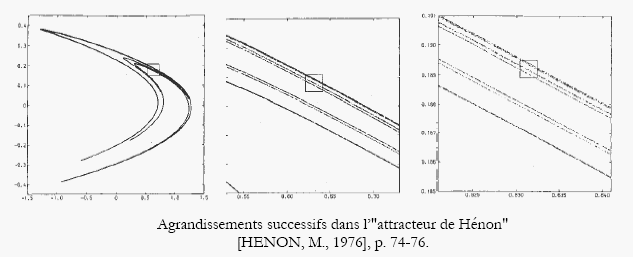
Tout l’intérêt du système de Hénon réside dans la facilité de programmer cette opération extrêmement simple, une itération à deux dimensions, simulant les comportements plus complexes des systèmes du type Lorenz 458 . Il devient un système numérique de référence, une sorte de modèle sur lequel un maximum de conjectures sont testées numériquement, comme le système de Lorenz qui a fait l’objet de nombreuses expériences numériques déjà en 1976 et continu de l’être, en parallèle du système de Hénon. Ainsi l’attracteur de Hénon est manipulé et les ensembles de Cantor sont visualisés avec leur structure auto-similaire 459 .
D’autres comportements sont mis en évidence. Pour b=0,3 par exemple, la forme de l’attracteur évolue de manière significative selon les valeurs de a : pour a petit, l’attracteur est un point, et lorsque a augmente il se transforme successivement en 2 points, puis 4, 8 et ainsi de suite par doublement 460 . Hénon rapproche la situation de celle évoquée par May en 1976, et annonce l’existence d’une valeur critique a c=1.06 pour laquelle il affirme obtenir un attracteur étrange.
Cet exemple illustre également les problèmes posés par une analyse à base de calculs numériques. L’ensemble de Cantor, l’attracteur étrange du système, ne sont que le résultat de calculs et un doute est émis quant à l’existence mathématique de l’objet : ne pourrait-il s’agir d’une orbite de période très longue plutôt que d’une non périodicité ? C’est une réflexion du mathématicien Sheldon Newhouse 461 qui jette le doute. Deux pistes d’analyse peuvent être suivies pour répondre à l’interrogation : soit s’engager dans une analyse mathématique, avec des outils très évolués pour démontrer l’existence ou non de l’ensemble de Cantor, soit rester dans la voie numérique pour déterminer l’éventuelle période de cette orbite de période très longue. Mais cette seconde voie débouche sur un écueil : les erreurs de calcul et d’arrondis, inévitables, empêchent l’évaluation numérique de la période 462 .
C’est là un problème très général avec les attracteurs étranges, amené par la proposition de Ruelle et non résolu depuis : il n’existe aucune preuve mathématique de leur existence, seulement des indications numériques (graphiques), même pour les plus étudiés d’entre eux 463 . Cela signe une certaine "limite" aux expériences numériques dans le domaine. Un seul système fait exception, celui construit par René Lozi 464 , mathématicien à l’université de Nice, à partir de l’attracteur de Hénon :
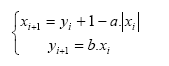
Il est un peu plus simple que les autres et le mathématicien Michal Misiurewicz est parvenu à démontrer, grâce aux outils des systèmes dynamiques, l’existence effective de l’attracteur étrange 465 .
Ces quelques exemples nous montrent l’épanouissement de la notion d’attracteur étrange, à la frontière des analyses numériques et des mathématiques des systèmes dynamiques. L’ensemble de Cantor est visualisé sur l’attracteur de Hénon et le travail numérique réalisé sur ce système est peut-être encore plus spectaculaire que ce qui touche à l’attracteur de Lorenz. En revanche, il existe des études de mathématiques avancées, une perspective topologique sur l’attracteur de Lorenz dès 1976, alors que l’attracteur de Hénon n’a pas encore été proposé ni publié.