Explications et détails techniques

Notre objectif désormais est double. D’une part nous voulons d’abord montrer les liens conceptuels ainsi que les similarités dans l’analyse de la stochasticité des systèmes conservatifs et du chaos, de manière à préciser les vagues parallèles que nous venons d’établir. D’autre part, on esquissera l’horizon historique dégagé en conséquence. Tout ceci sera prolongé par l’analyse du texte de Helleman.

Au préalable, quelques notions techniques minimales sont nécessaires pour comprendre les véritables enjeux du texte, à un niveau plus détaillé que les précédents éléments indicatifs. Nous avons choisi de suivre en grande partie la présentation de Chirikov, pour les notions d’intégrabilité, de séparatrice (et des homoclines associées) et de résonances.

En premier lieu, il convient de distinguer deux types de systèmes Hamiltoniens : les systèmes dits intégrables , et les autres, non intégrables. Un système d’Hamiltonien H, à n degrés de liberté :

En effet, dans ce cas le système s’intègre par quadrature et, sous certaines conditions, il existe des coordonnées dites "action-angle" (I, φ) telles que l’équation du mouvement se réduit à :

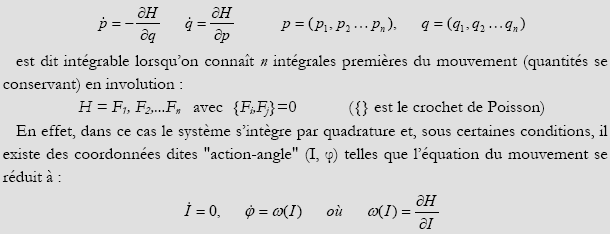
Sous ces mêmes conditions, le mouvement se fait sur un tore à n dimensions et il est quasi-périodique. Schématiquement on peut dire que les systèmes intégrables sont simples et leurs comportements sont connus. Les autres sont mal compris. La Mécanique classique est focalisée sur la recherche des systèmes intégrables, la question des oscillations non linéaires est centrée sur les systèmes non intégrables. Comme le dit Chirikov, la première catégorie est "exceptionnelle" et les problèmes qui l’occupent n’en font pas partie ⁴⁷³ .

Les situations intéressantes du point de vue dynamique correspondent au voisinage des séparatrices. Dans le cas d’un pendule simple, la situation est facile à comprendre : il s’agit de la trajectoire de l’espace des phases qui séparent deux comportements qualitativement totalement différents, l’oscillation et la rotation. Cette circonstance est remarquable car il suffit d’une toute petite perturbation à cet endroit pour faire basculer le comportement de l’oscillation à la rotation et inversement. L’Hamiltonien sous sa forme générale s’écrit, sous forme réduite, (p est le moment angulaire, φ l’angle, U₀ l’amplitude de l’énergie potentielle) :

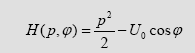
Les séparatrices correspondent à H=U₀ et ont pour équation : p_sx= ±2ω₀cos(φ₀/2).

Le diagramme de l’espace des phases est de la forme :

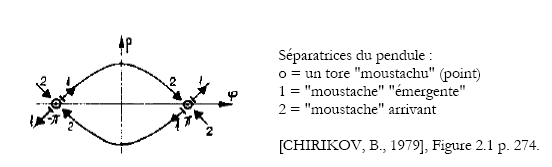
En reprenant Chirikov :

‘"Selon la terminologie de Poincaré, les moustaches sont appelées trajectoires doublement asymptotiques puisqu’elles approchent une trajectoire dans les deux directions du temps (t→±∞). Pour notre système, cette trajectoire limite – les points fixes instables φ=±π – est la même pour les deux limites t→±∞. Dans ce cas les moustaches sont appelées trajectoires homoclines." ⁴⁷⁴ ’

Il reste à donner des indications relativement au problème des résonances. Les oscillations libres d’un système Hamiltonien (pendule) sont stables et ne sont pas d’un grand intérêt ici. La recherche sur les oscillations non linéaires s’intéresse davantage à ce qui se passe lorsque le système est perturbé de la manière suivante :

H(I, φ ,t)=H ₀ (I) + ε .V(I, φ, t)avec ε petit.

Dans le cas où la perturbation est en plus périodique, dépendant périodiquement de la phase τ=Ωt+ τ ₀ , il est possible de développer la perturbation en série de Fourier :

Plus la phase mφ+nτ est petite, plus la perturbation a de l’effet. Dans le cas limite d’une phase constante, les résonances correspondent à mω(I)+nΩ=0. Ces fréquences ω _mn de résonances forment généralement un ensemble infini, dense (dans l’ensemble des ω ), ce qui explique l’intérêt pour les interactions entre ces résonances, problème de fond abordé par Chirikov.

Dans le cas simplifié où une seule résonance intervient (une seule composante dans la série de Fourier) il est possible de donner quelques caractéristiques (approchées) de la résonance. Avec un Hamiltonien de la forme

H(I, φ , τ )=H ₀ (I) + ε.V _mn (I)cos(m φ -n τ )

une approximation du type pendule est imaginable, c’est-à-dire qu’il est possible de trouver un Hamiltonien approchant, obtenu par transformation du premier, et de la forme :

H_r(p, ψ)=p²/2M+εV_mn(I_r)cosψ

Les séparatrices pour ce système ont alors pour équations :

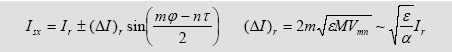
(I_r est une constante, α est un paramètre servant à caractériser la non linéarité des petites oscillations)

L’amplitude des oscillations (ΔI_r) est appelée demi largeur de résonance (en I) et nous allons voir comment elle entre dans la caractérisation du problème de stochasticité.