Détails sur le théorème KAM 479
En substance le théorème KAM présenté par Chirikov, avance un ensemble de résultats au sujet du comportement d’un Hamiltonien intégrable, à n degrés de liberté, perturbé de manière non intégrable (pour simplifier nous choisissons le cas autonome, c’est-à-dire que le temps n’intervient pas explicitement dans la formulation). Un tel système est de la forme :
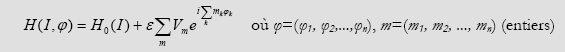
La perturbation a deux effets (sous certaines conditions bien évidement) :
• des tores invariants 480 pour le système intégrable non perturbé se déforment, mais conservent la forme de tore et restent invariants : ce sont les tores non résonants.
• les autres tores "explosent", car rien n’assure leur conservation, même sous la moindre perturbation : ce sont les tores résonants.
Tout dépend des fréquences (ω i ) (i=1..n) constitutives des tores. Lorsqu’elles vérifient une condition de résonance (amenée par la perturbation) Σ i m i ω i =0, la situation est critique au sens où les procédés de transformations successives évoqués ne sont absolument pas convergents : il se produit une éclatement du tore, quelque soit l’ampleur ε de la perturbation. Pour être exact, les changements de variables invitent des "petits dénominateurs" dans les séries, lesquels sont de la forme 1/ Σ i m i ω i . A la résonance même, le dénominateur s’annule. Tout le problème est de déterminer ce qui se produit à proximité de la résonance, lorsque le dénominateur est petit, mais pas nul (donc d’inverse grand). Est-il possible que le procédé converge malgré tout ?
La réponse est oui, les tores sont alors conservés, sous certaines conditions, qui correspondent à la définition d’un voisinage "interdit" des résonances (appelé couche de résonance par Chirikov 481 ) et d’une amplitude ε maximale pour la perturbation. Hors de cette zone il y a stabilité.
Ce résultat ne résout pas tous les problèmes, mais établit la coexistence de stabilité et d’instabilité, dans des systèmes d’oscillations non linéaires, issus de systèmes intégrables faiblement perturbés. Par ailleurs, dans le cas général, la catégorie des tores résonants occupe la majeure partie de l’espace des possibles. En effet, les zones interdites forment des couches autour des résonances qui elles-mêmes couvrent l’espace des (ω i ) de manière dense. Ceci a pour conséquence qu’il est quasiment impossible de choisir les conditions initiales du système dans un "bon" domaine, c’est-à-dire une zone de stabilité.