d. La notion de chaos dans les travaux de Rössler

En analysant ces travaux abondants, nous avons parfois pris la peine de révéler ce que cachait le terme chaos. Revenons maintenant plus en détail sur les spécificités de la construction de la notion de chaos et son utilisation par Rössler, afin de souligner les nuances par rapport aux autres conceptions contemporaines.

Tout d’abord, la transposition du chaos, du discret au continu, qui est un apport essentiel du travail de Rössler, n’est pas évidente. Rössler utilise des analogies graphiques et travaille sur des modèles de papier pour procéder au transfert de la notion de chaos "à la Li-Yorke" au "chaos continu". La transposition inclut les propriétés associées aux itérations discrètes : orbites périodiques en nombre infini, trajectoires non périodiques en quantité non-dénombrable, instabilité des trajectoires.

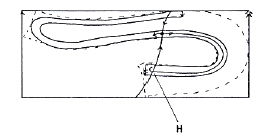
Ainsi Rössler généralise la notion de Li et Yorke en reprenant les caractéristiques de mélange d’orbites périodiques et non périodiques. Malgré ses longs développements théoriques et l’évolution des résultats, il n’a pas perdu son idée de départ ⁵⁹³ . En étant plus précis, sur les modèles papiers, ces idéalisations des processus dynamiques, les lignes qu’on peut dessiner sur le papier correspondent aux orbites périodiques ou non périodiques du cas discret. Il y a une relation univoque entre les endomorphismes à une dimension et les "origamis avec des lignes" ⁵⁹⁴ . Dans ce cadre abstrait, on comprend facilement l’extrapolation de Rössler. Cependant, une fois sorti de ces modèles abstraits, dans la recherche de systèmes différentiels, non idéalisés, par l’intermédiaire de la théorie des oscillations chimiques, Rössler est conduit à des comportements plus complexes. Que reste-t-il du chaos proposé par Li et Yorke ?

Tout repose alors sur les notions de Smale et les propriétés du fer à cheval : celui-ci génère un comportement "équivalent" à celui de Li et Yorke, et un mélange aussi complexe de trajectoires périodiques et non périodiques. Ainsi la définition de chaos dans ce cadre n’a pas à être modifiée. Ceci explique pourquoi Rössler emploie toujours l’expression de "trajectoire non périodique" comme synonyme du terme chaos ; il se réfère par là à la fois à Li et Yorke, au travail de Lorenz ⁵⁹⁵ et à celui de Smale.

Force est de constater que sa démarche se démarque de celle de Ruelle. Il ne s’agit pas de transférer des notions de mathématiques des systèmes "Axiome A" vers des systèmes différentiels du type de Lorenz. D’autres points sont frappants. Tout d’abord, la notion de sensibilité aux conditions initiales n’est jamais vraiment mise en avant. Elle est présente, mais toujours en arrière plan, alors qu’elle a tendance à prendre le dessus au fil du temps chez d’autres chercheurs du domaine. L’instabilité des orbites périodiques, la sensibilité aux conditions initiales sont des éléments présents en filigrane, mais ne sont pas les aspects primordiaux du concept de chaos. Le fait qu’il ne produise aucune étude des exposants de Lyapounov des systèmes n’a rien d’étonnant et traduit un certain désintérêt pour la chose.

Cela ne signifie pas qu’il ne se rend pas compte de l’existence et de l’importance d’une telle sensibilité ⁵⁹⁶ . Pour Rössler, elle n’a de sens qu’à travers les mécanismes de génération de chaos. La sensibilité aux conditions initiales se manifeste à travers la notion d’étirement-repliement dans le fer à cheval ou la transformation du boulanger, et non pas comme divergence exponentielle de trajectoires voisines. L’"hyperbolicité", au sens d’une combinaison d’étirement et de repliement, est l’élément clé, utilisé dès 1976 dans son "mélangeur".

On remarquera également qu’il reste prudent avec la notion d’attracteur étrange. Pour Rössler, le chaos ne se limite pas à l’existence d’un attracteur étrange, comme l’ont défini Ruelle et Takens en 1971. La présence de cet objet géométrique implique l’existence d’un chaos, au sens de la coexistence d’orbites périodiques et non périodiques,

‘"cependant la réciproque n’est pas vraie : le nombre de systèmes ‘presque chaotiques’ est beaucoup plus grand, par exemple en chimie, que ceux qui possèdent un attracteur étrange." ⁵⁹⁷ ’

C’est pour cela qu’il distingue une notion d’"attracteur chaotique" à côté de celle d’"attracteur étrange" ⁵⁹⁸ . Mais il signale immédiatement après que cette distinction n’est pas vraiment viable au niveau pratique, car un petit bruit suffit à rendre ces différences imperceptibles (physiquement, chimiquement et aussi numériquement). La divergence de conception est tout de même significative.

De même, tous les aspects liés à des questions de hasard et d’aléatoire sont écartés chez Rössler. Li et Yorke, May, les physiciens plus proches de la Mécanique statistique et quelques autres n’ont pas manqué d’y faire référence, mais Rössler s’en éloigne et "son" chaos relègue cette dimension en arrière-plan :

‘"Le chaos génère de l’aléatoire (imprédictibilité), et peut être caractérisé, dans une certaine mesure, par des méthodes statistiques. D’un autre côté, il est bien moins grossier que ce que pourra jamais devenir une méthode statistique quelconque." ⁵⁹⁹ ’

Le chaos pour Rössler s’insère bien au contraire dans l’idée de comportement dynamique au sens d’une oscillation complexe, d’une "super-oscillation". Il considère que l’état d’équilibre est le comportement type de la dimension un, l’oscillation celui de la dimension deux (avec la limite imposée par le théorème de Poincaré-Bendixon) ⁶⁰⁰ . Le chaos apparaît comme le phénomène caractéristique de la dimension trois ⁶⁰¹ . Le principe de réinjection assure le passage à une dimension supérieure, de la première à la deuxième, de la deuxième à la troisième. L’hyperchaos est l’extension du processus à la dimension quatre.