c. Mitchell Feigenbaum et l’universalité

Dans le chapitre des itérations la contribution de Feigenbaum est importante. Il a promu, en effet, l’universalité à un rang très élevé dans les préoccupations des systèmes dynamiques. Nous allons montrer, en analysant son parcours, que Feigenbaum adopte un point de vue de physicien sur les itérations, permettant de donner un sens nouveau à cette universalité et de produire des résultats assez spectaculaires.

L’idée de l’universalité, l’indépendance par rapport à la fonction itérée, lui vient directement de Paul Stein (du groupe Metropolis, Stein et Stein). Ces premiers pas dans les itérations lui ont été inspirés par une présentation de S. Smale au Center for Physics à Aspen (Colorado, Etats-Unis), en 1975. Feigenbaum entreprend alors d’étudier les itérations quadratiques (du type x _n+1 =λ.x _n (1-x _n )) ⁷²⁰ . Le doublement de période est analysé sur une calculatrice HP-65, assez lente : c’est de cette manière que Feigenbaum se familiarise avec le processus de convergence des valeurs λ _n du paramètre λ, pour lesquelles il se produit un doublement, vers la valeur critique λ _c (à partir de laquelle il y a chaos, selon les conceptions de Li et Yorke). La convergence géométrique des λ _n lui apparaît sur ce tout premier exemple. En déterminant de manière précise la raison géométrique il trouve :

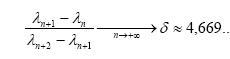
P. Stein lui annonce alors que le doublement de période existe pour toute une classe d’itérations. Quelques temps plus tard, Feigenbaum décide donc de faire les calculs sur une seconde itération (x _n+1 =λ.sin(πx _n )), pour laquelle il retrouve le même phénomène de convergence géométrique et la même raison géométrique, ce qui constitue la grande surprise : δ = 4,669…

Vers 1976 donc l’universalité réapparaît dans le domaine ⁷²¹ . Mais il existe une différence avec les précédentes tentatives. Avec Metropolis, Stein et Stein, il s’agissait d’avoir une idée qualitative de l’évolution de l’itéré d’un point. Feigenbaum souligne le caractère quantitatif des nouveaux résultats : la "théorie de l’universalité montre que des équations qualitativement semblables ont le même comportement quantitatif" ⁷²² .

Pour être plus précis, nous dirons que Feigenbaum met en lumière un phénomène invariant d’échelle, renvoyant à une régularité cachée. Ce sont les connaissances en matière de phénomènes critiques et de théories de renormalisation qui autorisent Feigenbaum à une telle lecture des phénomènes. Une étape nouvelle est en train d’être franchie à propos de la cascade de doublements de période. Il reste à donner un cadre théorique, permettant à la fois d’expliquer cette universalité et de démontrer les propriétés indiquées par un ensemble de résultats numériques. Car Feigenbaum choisit et observe numériquement ces phénomènes mathématiques pour "créer de l’intuition" ⁷²³ .

A la fin de l’année 1976, l’essentiel des explications est échafaudé. De manière heuristique, puisque c’est ainsi que Feigenbaum le présente dans un premier temps, nous donnons l’opération de base, qui donne lieu à l’invariance d’échelle, reconnue dans le doublement de période d’une itération notée x _n+1 = λ.f(x _n ).

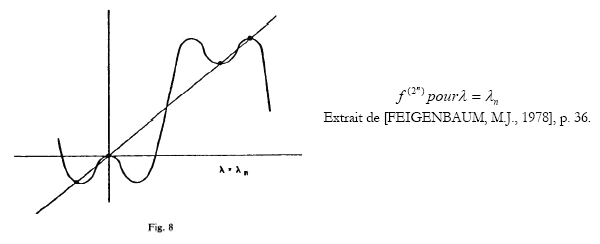
En notant l’itération de manière plus synthétique x _n+1 =h(λ,x _n ) et en introduisant F(n,λ,x)=h (n) ( λ,x)=h(λ,h(λ,…h(λ,x)…)), la formulation mathématique est une fonction T incluant le décalage de λ, et la double transformation géométrique (renversement, changement d’échelle par un facteur α), agissant directement sur les fonctions ⁷²⁴  :

La formulation s’exprime en termes analogues à une transformation de groupe de renormalisation. Elle a été proposée grâce à l’aide de Pedrag Cvitanovic, en situation post-doctorale en physique à Los Alamos à ce moment là ⁷²⁵ . Ceci permet de voir le paramètre λ comme une température, le point de basculement vers le chaos comme un point critique d’une transition de phase, et la raison géométrique δ comme un exposant critique de cette transition. Publié seulement en 1979, suite à de nombreuses difficultés pour faire accepter un article ni mathématiquement rigoureux, ni vraiment de physique statistique, ceci n’est encore qu’une première étape : le résultat (l’universalité) n’est pas démontré, mais présenté sous forme de conjecture. La première preuve, pour une certaine classe d’universalité seulement, est le fait d’Oscar Lanford III, en 1981. Mais la démonstration est encore assistée par l’ordinateur pour réaliser des calculs ⁷²⁶ . Le travail de Pierre Collet, Jean-Pierre Eckmann et Oscar Lanford, publié en 1980, constitue la première preuve mathématique d’une universalité : leur but est de "montrer que l’explication de Feigenbaum est correcte, au moins dans certains régimes limités" ⁷²⁷ .

Malgré leurs approximations, l’universalité et le formalisme de Feigenbaum parviennent à se faire une place dans le champ du chaos à partir de 1977. C’est surtout son intervention au colloque de Côme, durant l’été 1977, qui est saluée et enfin appréciée à sa juste valeur ⁷²⁸ . Par ailleurs, le résultat de Feigenbaum est signalé dans l’autre grande conférence du moment, à New York, par l’intermédiaire de John Guckenheimer ⁷²⁹ . Le succès de Feigenbaum est quasiment assuré dès 1978, au point de rapidement occulter certaines contributions pourtant significatives. Ce sont deux français, Coullet et Tresser, travaillant à Nice, qui font les frais de cette focalisation sur Feigenbaum. Deux autres chercheurs de Toulouse, Christian Mira et Igor Gumowski ont eux aussi abordé la question du doublement de période, selon une approche originale, un peu passée sous silence. C’est en comparant ces différents résultats que nous ferrons ressortir les traits saillants de chacune des démarches et surtout leur rapport au chaos.