a. Les différences d’approche avec Feigenbaum

Tout d’abord, l’intérêt suscité par la question n’a pas la même origine que chez Feigenbaum ⁷³² . Au laboratoire de Nice, Coullet travaille avec Jean Coste et Jean Peyraud (directeur du laboratoire) sur les instabilités de modes en dynamique des fluides. Dans le cas d’un écoulement de Bénard, une première analogie avec une dynamique de populations en compétition est construite ⁷³³ .

Un écoulement de Bénard dans une lame de fluide initialement isotrope est sujet à des modes hydrodynamiques fluctuants, de type rouleau, orientés selon différentes directions (ou angles) θ _i autorisées par les conditions aux limites. Une modélisation du système, en prenant en considération l’intensité x _i de ces modes instables, permet de mettre le système en correspondance avec un modèle de compétition entre autant d’espèces, de populations x _i , du type des systèmes de Volterra. Le but de l’opération est d’étudier les mécanismes de sélection de modes qui apparaissent en grand nombre dans un écoulement de type Bénard. Le modèle de fluide choisi est donc une équation de Volterra avec quelques conditions supplémentaires sur les coefficients. Une partie des résultats connus pour le système de Volterra peut être transférée au cas hydrodynamique.

Par le biais de cette analogie, la question de l’analyse non linéaire d’une dynamique compétitive est posée. L’analyse linéaire de stabilité du système ne permet que des conclusions très limitées. Une analyse utilisant les ressorts des systèmes dynamiques est envisagée. Le premier constat est que, dans le cas particulier de l’écoulement de Bénard (qui est symétrique), la dynamique conduit à la convergence vers un mode instable (sélection d’une espèce) et à l’élimination de tous les autres : ceci correspond à la configuration stationnaire de l’écoulement.

Le système de Volterra est étudié de manière plus générale. D’où l’intérêt pour les résultats publiés en 1975 et dus à Robert May et Warren Leonard, du département de biologie de Princeton. Sur un système de trois espèces May et Leonard ont trouvé, numériquement, un comportement pathologique, qui oscille indéfiniment entre les trois points N ₁ , N ₂ , N ₃ chacun représentant l’existence d’une unique espèce parmi les trois. Leur analyse mathématique permet de caractériser cette dynamique.

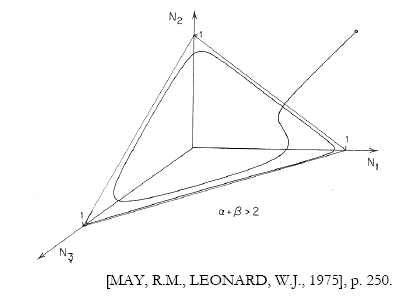
La complexité du phénomène est intéressante mais comme l’affirment May et Leonard :

‘"Biologiquement, le comportement illustré [sur la figure précédente] est un non-sens. Mathématiquement, pour des variables continues N _i (t), le système n’atteint jamais asymptotiquement aucun des points (1,0,0), (0,1,0), (0,0,1), […] Ce qui reste d’intéressant dans cette analyse est l’observation générale que des non linéarités peuvent produire des phénomènes cycliques non périodiques…" ⁷³⁴ ’

Dans le cas de la Mécanique des fluides, il existe un analogue simple de ce résultat : dans un modèle de convection en rotation, il s’agit des basculements de l’angle de l’axe θ _i entre trois configurations. La situation présentée par May et Leonard est plutôt académique (cela suppose une symétrie de permutation) et le modèle de fluide rentre plus naturellement dans cette catégorie (symétrie de rotation) qu’un modèle de populations.

Avec l’appui d’Alain Chenciner, mathématicien déjà aguerri aux méthodes des systèmes dynamiques, plusieurs cas d’équations différentielles de compétitions d’espèces sont alors étudiés ⁷³⁵ . Plus que les résultats en eux-mêmes, ce sont à la fois les connaissances acquises au sujet des systèmes dynamiques et la série de coïncidences qui se développent à partir de cette question d’évolution des populations biologiques, qui sont importants.

D’après Coullet, Jean Peyraud est allé présenter leurs travaux à l’Observatoire de Nice, où il a des contacts et où travaille Michel Hénon ⁷³⁶ . Ce dernier les a orientés vers un autre article, alors tout récent, de Robert May : celui de 1976, paru dans Nature et décrivant toute la série des résultats connus au sujet des itérations unidimensionnelles (elles-mêmes utilisées pour modéliser des populations en biologie) dont les propriétés de la fonction logistique et le doublement de période.

Sur la base de l’article de May, Coullet réalise des tracés (sur une table traçante Hewlett-Packard) de l’itération de la "bosse" (fonction logistique), pour différentes valeurs du paramètre. L’objectif était d’en faire un séminaire ⁷³⁷ pour présenter tous ces résultats nouveaux. En laissant tourner les calculs pour la 512ème (ou 1024ème) itérée de la fonction, l’image alors obtenue, au point critique, est visuellement auto-similaire. Avant ce point la figure est plutôt lisse.

Les réactions de Coullet et Tresser sont assez immédiates. La ressemblance avec une transition comme on peut en trouver en physique des phénomènes critiques leur vient à l’esprit rapidement ⁷³⁸ . En conséquence il restait à déterminer si, au-delà de l’image, ce phénomène a les caractéristiques d’une "vraie" transition : dans quelle mesure y a-t-il universalité et peut-on formuler une théorie avec le groupe de renormalisation ? Pour Coullet et Tresser il y a beaucoup d’enthousiasme, peu de certitudes, mais une forte conviction et de grands espoirs suscités par toute leur culture de la physique des transitions de phase. Les analyses poussées ne sont faites que durant l’été 1977, période plus propice à ces recherches peu académiques, et durant laquelle les machines à calculer sont accessibles plus facilement ⁷³⁹ .

A leur dire, leurs premières tentatives visent à mesurer la dimension de Hausdorff de la figure tracée, pour différents profils de la bosse ⁷⁴⁰ , afin de tester l’universalité des figures auto-similaires. Mais les résultats sont peu probants, puisque rien d’universel n’est détecté a priori. Ce n’est qu’à la suite de l’idée de Tresser de considérer la dimension de Hausdorff comme seulement locale et répartie elle-même selon un ensemble de Cantor ⁷⁴¹ , que la situation se débloque.

L’étape de la formulation en terme de groupe de renormalisation n’intervient qu’après l’accumulation de suffisamment d’indices d’universalité. Pour résumer ces premiers pas :

‘"Ces résultats numériques suggèrent une forte analogie avec les phénomènes critiques (divergence de certaines quantités comme le nombre de points de l’orbite lorsque R -> R_c, une certaine notion d’invariance d’échelle associée à la structure d’ensemble de Cantor, universalité). Nous nous proposons de comprendre ces résultats à l’aide d’une technique en tout point analogue à celle du groupe de renormalisation introduit par Wilson-Kadanoff dans l’étude des phénomènes critiques." ⁷⁴² ’

Le mécanisme d’apparition de l’ensemble de Cantor est ainsi traité comme une transition de phase : formulation en groupe de renormalisation, détermination de son point fixe, calcul des exposants critiques.

Le groupe de renormalisation est construit d’après la comparaison suivante : la bosse R1 (voir figure ci-dessous) de l’itéré f (2) est un analogue de la courbe de départ f, moyennant un changement d’échelle.

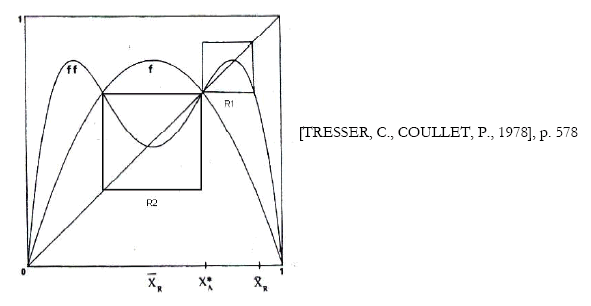
Au-delà des différences circonstancielles, la première distinction avec la formulation de Feigenbaum apparaît dans le choix opéré. En adaptant les explications de Feigenbaum au schéma présenté, Feigenbaum prend la bosse R2, sur laquelle il produit un renversement et un changement d’échelle pour trouver l’analogue de la bosse initiale (L’opération de renormalisation ne possède que ces deux générateurs et les possibilités sont épuisées).

Guidés par leur analogie, Coullet et Tresser s’intéressent au comportement de divergence de la période :

Tels qu’ils sont publiés après septembre 1977, ces résultats renvoient directement à l’interprétation de Feigenbaum. Coullet et Tresser ont été informés par l’intermédiaire de Michel Hénon, une nouvelle fois : celui-ci était présent à Côme durant l’été 1977, où Feigenbaum fût "célébré" et a obtenu un prétirage de l’article de Feigenbaum (qui ne sera publié qu’en 1978).

Coullet et Tresser sont engagés dans une voie de type Mécanique statistique, leur indiquant les hypothèses à poser (celles courantes en renormalisation ⁷⁴⁴ ) et comment interpréter l’universalité et les exposants critiques. La série géométrique de Feigenbaum n’est qu’une incarnation de leur vision en terme de phénomène critique. Aussi peuvent-ils donner la valeur δ de Feigenbaum. Mais il faut bien souligner que le caractère géométrique n’est qu’une variante de l’exposant critique, plus fondamental.

L’analogie avec la transition de phase va déjà beaucoup plus loin : non seulement, il se produit une cascade de doublements de période avant le point critique, mais il se produit une cascade inverse, après le point critique. Ce comportement est courant dans les transitions de phase en physique et, comme en physique, l’exposant critique est le même des deux côtés, universellement. Coullet et Tresser perçoivent donc de manière plus générale ce que Feigenbaum a entr’aperçu et l’insèrent dans un cadre explicatif. On peut noter que Grossman et Thomae ⁷⁴⁵ avaient également perçu la cascade et son miroir en 1977, sans chercher quoi que ce soit d’universel. E. Lorenz a retrouvé la cascade inverse en 1980 ⁷⁴⁶ , mais en ignorant que Coullet et Tresser l’avait déjà compris.

Une série de calculs numériques tend par ailleurs à montrer un autre type d’universalité de classe ⁷⁴⁷ .

En effet, les exposants critiques dépendent de la classe de la "bosse", c’est-à-dire de l’ordre du zéro de la dérivée de la "bosse" en son maximum. A ce niveau, c’est la structure du Cantor au point critique qui est concernée : l’invariance d’échelle a des caractéristiques différentes selon les classes. La divergence à l’approche de R _c ne change pas.

Répétons le, tout ceci repose sur une analogie très suivie avec l’opération de renormalisation et de nombreux calculs numériques (tout comme Feigenbaum). Plusieurs éléments viennent renforcer leur conviction : la lecture de l’article de Metropolis, Stein et Stein de 1973 signalant une universalité et le théorème de Sharkovsky ⁷⁴⁸ . Coullet et Tresser donnent aussi le premier modèle très simple, exactement soluble, pour leur théorie, à partir de l’application :

B(x) = 2.xpour 0 ≤ x ≤ ½

B(x) = 2.(1-x)pour ½ ≤ x ≤ 1

donnant la famille à un paramètre f _R (x) = R.B(x), pour R dans [0,1]. ⁷⁴⁹

L’opération de renormalisation dans ce cas est simple, l’existence d’un point fixe est immédiate et, malgré une itération qui ne reproduit pas tout à fait le phénomène de doublement de période, le modèle démontre, en termes mathématiques, l’intérêt de l’approche en terme de groupe de renormalisation et indique d’où proviennent les lois d’invariance de type géométrique ⁷⁵⁰ . Là où Feigenbaum s’arrêtait à des conjectures, Coullet et Tresser proposent quelques éléments de démonstration.

Enfin, dans l’esprit de Coullet et Tresser l’universalité prend une autre dimension, non limitée au cadre des itérations. Ils prétendent notamment : "on est tenté de conjecturer une universalité quantitative pour des comportements turbulents plus réalistes dont la turbulence fluide n’est peut-être qu’un exemple particulier" ⁷⁵¹ .

Le raisonnement justifiant cette extension est explicité dans les comptes rendus du colloque de 1977 ⁷⁵² . Il s’appuie sur deux éléments essentiellement. Tout d’abord, le caractère discret des itérations étudiées n’a rien de "pathologique" : moyennant certaines conditions, elles peuvent, en effet, représenter une application de Poincaré d’un flot. L’attracteur de Hénon illustre cette possibilité car il est construit comme modèle simple reproduisant l’application de Poincaré du modèle de Lorenz. Ensuite, ils s’inscrivent dans ce nouveau contexte d’interrogation sur la turbulence : les idées de Ruelle et Takens sur la turbulence, les attracteurs étranges, le modèle de Lorenz (pensé à partir d’un système convectif). Feigenbaum, s’il perçoit l’importance de l’universalité, se détache plus difficilement du cadre des itérations ⁷⁵³ .