e. Chaos et transition vers le chaos, après 1980

A la fin des années 1970, pour Coullet, Tresser et Arnéodo, la question de la transition est clairement reliée à celle du chaos. La transition vers le chaos permet en effet de donner une idée du chaos auquel les transitions aboutissent et ils soulignent plus généralement l’importance de s’interroger sur l’origine et la nature du comportement chaotique ⁷⁸⁴ . A quelle notion de chaos font-ils référence et comment chaos et transition vers le chaos se répondent-ils ?

Pour les débuts, en 1977, il est difficile de répondre : il s’agit pour Coullet et Tresser d’un moment de découverte et, de manière diffuse, le chaos (qui est appelé turbulence) est un mélange de chaos selon Li et Yorke (et May, source primaire de leurs réflexions), de questions de stochasticité, de sensibilité aux conditions initiales, d’attracteur étrange ⁷⁸⁵ . Cependant, l’étude de la transition dans les itérations unidimensionnelles se focalise sur l’ensemble de Cantor qui concentre en quelque sorte ces ingrédients et donne la meilleure représentation de "leur" chaos : leur culture des transitions de phases leur fait certainement préférer cet objet invariant d’échelle, autosimilaire, fractal.

Par la suite, nous l’avons signalé, la définition d’un paramètre d’ordre, l’entropie topologique locale, va de paire ave une réévaluation de la notion de chaos. La structure précédente n’est pas caduque, mais, d’un point de vue pratique, il est plus efficace de recourir à cette caractéristique entropique, plus simplement discriminatoire d’une stochasticité. L’installation des mathématiques des systèmes dynamiques permet de préciser ces notions et finalement de superposer deux structures, métrique et topologique.

Tout ceci se passe dans le cadre des itérations et des applications de Poincaré de flots. L’intérêt pour les flots eux-mêmes, la résurgence de l’attracteur étrange dans leurs conceptions (non plus limité à sa trace sous forme d’ensemble de Cantor) signe une nouvelle étape, perceptible en 1981. A propos des études des systèmes où se présentent des phénomènes turbulents, chaotiques, ils précisent :

‘"L’annulation asymptotique des fonctions d’autocorrélation, la mise en évidence d’un spectre de bruit continu, la positivité des exposants de Lyapounov sont les tests de stochasticité utilisés. Il n’existe à l’heure actuelle aucune preuve (théorique) pour ces systèmes de l’existence d’attracteurs étranges." ⁷⁸⁶ ’ ‘"On peut se limiter à appliquer les tests numériques de stochasticité précédemment cités. On peut aussi s’aventurer à essayer de démontrer l’existence mathématique d’attracteurs étranges." ⁷⁸⁷ ’ ‘"Dans certains cas […] il est cependant possible soit de définir des flots modèles pour lesquels on sait démontrer l’existence d’attracteurs étranges : c’est la méthode qu’ont utilisée Guckenhermer (sic)- Parry-Williams dans l’étude de l’attracteur de Lorenz ; soit d’utiliser des théorèmes généraux dus essentiellement à Shil’nikov et qui permettent de comprendre l’origine et la structure des comportements chaotiques." ⁷⁸⁸ ’

Plusieurs remarques s’imposent. Jusqu’à présent, il n’a jamais été question des tests numériques à partir des exposants de Lyapounov, spectres, etc. Leurs connaissances sont suffisantes pour que cette mise à l’écart ne soit pas le fait d’une méprise. Cela est parfaitement assumé et ces calculs n’ont qu’un intérêt limité ; Coullet et Tresser ont déjà leur critère de stochasticité. Plus que cela, de tels indices ne servent pas à répondre à la question de l’origine et la nature du chaos, ni à celle des scénarios de transition. On peut ajouter que les calculs de dimension d’attracteur étrange sont également évacués, sans doute pour la même raison.

Deuxièmement, l’annonce de 1981 (mûrie antérieurement) se traduit concrètement par de nouvelles perspectives en termes de recherches et de résultats. La conception de chaos en tant qu’attracteur étrange aboutit à la construction d’un nouveau scénario. L’exemple le plus significatif est l’article au titre révélateur : "A possible new mechanism for the onset of turbulence", publié en 1981. Comme le titre l’indique il est d’abord question d’un mécanisme de transition vers la turbulence, mais le cadre n’est plus celui des itérations discrètes : il s’agit de familles paramétrées de flots Φ _a à trois dimensions (avec une condition de symétrie). Court mais fourmillant d’idées, il illustre tout le rapport entre une conception de chaos et une transition.

En s’inspirant de la méthode de Guckenheimer-Williams, Arnéodo, Coullet et Tresser ont en effet échafaudé un nouveau scénario de transition continue vers la turbulence, sous forme d’une cascade, où intervient une succession d’orbites homoclines, dont la forme se complique avec le paramètre a. Plus précisément, la transition suit le scénario suivant :

• il existe des valeurs (ã _n ) de a pour lesquelles Φ _a possède une paire d’orbites homoclines (à O) stables,

• pour a≥ ã _n (et a≈ ã _n ) une orbite périodique symétrique est générée par bifurcation des précédentes homoclines,

• pour a=a _n є]ã _n , ã _n+1 [ l’orbite périodique est déstabilisée et donne naissance à deux orbites périodiques stables, symétriques l’une de l’autre,

• une nouvelle bifurcation à a= ã _n+1 ramène à une situation à deux homoclines.

• La succession se répète jusqu’à une limite a _∞ = lim_n→∞ a _n = lim_n→∞ ã _n , au-delà de laquelle il y a chaos.

Selon la procédure de Guckenheimer-Williams pour le flot de Lorenz, ils ont construit une suspension (un flot dans R 3) de l’application :

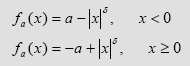
Le diagramme de bifurcation, le mécanisme de transition, la formulation en groupe de renormalisation sont transférés grâce à la même procédure de suspension d’une application en flot : les résultats connus pour les itérations ont leur pendant dans le cadre des flots. Ceci explique le choix de l’application f _a : il s’agit de la famille faisant l’objet de la démonstration de Collet, Eckmann, Lanford, à propos de la résolution des équations de renormalisation.

On peut signaler également que les résultats sont bien différents dans le cas des flots par rapport aux itérations, au moins sur deux points :

• il n’y pas de doublement de période (d’orbites périodiques) et pas de pics dans le spectre associé. Au contraire, puisqu’il s’agit d’homoclines, c’est la fréquence zéro qui prédomine, et ce pic de fréquence devrait être largement prépondérant.

• il y a universalité (même loi d’échelle pour a _n et ã _n ) mais δ dépend d’un certain nombre de paramètres des flots construits. Pas question d’une "super-universalité" comme c’est le cas des itérations avec le paramètre δ de Feigenbaum : il s’agit de multiples classes d’universalité contiguës (car dépendant continûment des paramètres des flots).

Quelles conclusions tirer de l’analyse de cet article ? On comprend d’abord que la notion de chaos ne se limite pas à une question d’entropie topologique, plus propre aux itérations. Si l’entropie topologique positive reste un moyen de caractérisation du chaos, la notion d’attracteur étrange et les orbites homoclines ont toute leur importance. Le chaos est une véritable superposition de structures et devient une notion toujours plus sophistiquée.

L’article marque également l’éventualité d’étendre les techniques de renormalisation et les propriétés d’universalité hors des itérations, directement dans les flots.

Enfin, et il faut insister sur ce point, les auteurs manipulent des modèles de flots, construits selon les prescriptions de Guckenheimer et Williams notamment. Ce choix s’explique dans la mesure où ils pensent que les attracteurs étranges sont des bons éléments pour étudier les comportements chaotiques mais qu’il faut dépasser le cadre théorique, mathématique, reposant sur les considérations de systèmes dynamique Axiome A car :

‘"[…] cette théorie ne nous permet pas de comprendre la stochasticité générée dans les analyses numériques de difféomorphismes et équations différentielles donnés par des expressions algébriques explicites." ⁷⁸⁹ ’

Ainsi les "modèles topologiques" ⁷⁹⁰ ouvrent des nouvelles possibilités. On notera cependant, que les démonstrations sont très heuristiques, relayées comme d’habitude par des calculs numériques sur des systèmes différentiels suffisamment représentatifs des propriétés annoncées. En outre, il est problématique de trouver des exemples numériques précis. Nous ne pouvons manquer de rapprocher cette perspective de celle de Rössler, quelques années auparavant, dans les méthodes et les pratiques (en faisant abstraction des résultats à proprement parler). L’analogie avec sa démarche ne s’arrête pas là.

A côté des méthodes de Guckenheimer-Williams, nous avons mentionné leur choix de recourir aux théorèmes de Shilnikov. L’intérêt pour ces théorèmes peut se résumer par cette citation de l’article explicitant la problématique et les premiers résultats de Arnéodo, Coullet et Tresser en la matière :

‘"Une étape fondamentale dans l’étude de la stochasticité dans de telles équations différentielles consiste à prouver l’existence d’une infinité d’orbites périodiques isolées. Cependant, il semble douteux sinon sans espoir de trouver des théorèmes généraux donnant des réponses définitives à ce dernier problème sous des conditions déterminables analytiquement. Le but principal de cet article est de donner des arguments convaincants au fait que l’origine et la structure des comportements chaotiques auxquels beaucoup de familles d’équations différentielles d’ordre trois à un paramètre sont sujettes, peuvent être compris à la lumière du théorème suivant, qui est une légère modification d’un ancien résultat de Shil’nikov." ⁷⁹¹ ’

Pour les niçois il ne fait aucun doute que

‘"[…] l’utilisation conjuguée de l’ordinateur, des méthodes de G-P-W et des théorèmes généraux dus essentiellement à Shil’nikov permettra de nouveaux progrès dans la compréhension des mécanismes conduisant à la turbulence." ⁷⁹² ’

Ils procèdent en deux temps. Ils illustrent d’abord l’application des théorèmes dans l’étude du chaos. Les conditions d’applications du théorème sont vérifiées soit analytiquement dans un cas simple, soit numériquement sur des systèmes plus explicites. Parmi ces systèmes, il y a ceux de Rössler destinés à illustrer les notions de chaos "de type vis" et "de type spiral". Les conditions du théorème sont presque vérifiées, mais les trois physiciens signalent : "il semble que Rössler ait déjà eu une l’intuition d’un tel phénomène" ⁷⁹³ . Ceci n’a rien d’un hasard et n’est pas anecdotique : fondamentalement, cela témoigne d’un cheminement tendant partiellement vers la perspective de Rössler. Par ailleurs, nous avons déjà signalé que les méthodes de Williams (et Guckenheimer) sont proches des modèles de papier de Rössler.

A la différence de Rössler cependant, leur perspective reste, dans un second temps, le problème de la transition vers le chaos, bien qu’il ne soit pas vraiment possible de dissocier ce problème de l’étude du phénomène de chaos. Ce qui explique les derniers mots de la conclusion de l’article de 1982.

‘"Plus précisément, lorsque Г ₀ [orbite homocline] existe, il y a un fer à cheval avec une infinité de branches dans une application de Poincaré typique pour le flot ; le nombre de branches décroît quand on déplace les paramètres hors des valeurs pour lesquelles une orbite homocline existe. Cette évolution explique que des phénomènes bien connus comme les cascades de bifurcations sous-harmoniques, ou l’intermittence, apparaissent naturellement quand on fait varier les paramètres dans de tels systèmes." ⁷⁹⁴ ’

Le monde des systèmes dynamiques domine donc leur perspective sur le chaos à base d’homoclines. Ce sujet des orbites homoclines est surtout développé ensuite par Charles Tresser après 1981 et divers travaux, dont sa thèse d’Etat, présentent les théorèmes de Shilnikov. Il propose aussi de classifier les flots sur la base de la topologie des homoclines étudiées ⁷⁹⁵ .