a. Observations et interprétations
Nous avons évoqué le constat, un peu inattendu, fait lors des simulations analogiques du "second" attracteur dans le système de Lorenz, par les physiciens Y. Pomeau et J.L. Ibanez, en 1976. Pomeau revient sur cette observation dans un article de 1980 :
‘"Dans les études systématiques du système de Lorenz sur un ordinateur analogique, j’avais remarqué une transition […] vers la turbulence que je n’avais pas vraiment comprise à cette époque. Il est intéressant cependant de citer les observations correspondantes pour éclairer ce mécanisme. Je suivais sur un écran de TV le point de coordonnées disons x(t), z(t) où l’évolution temporelle de x et y est gouvernée par l’eq. (1) [Lorenz]. Lorsqu’un cycle limite stable était atteint le calcul (analogique) était si rapide qu’il était impossible de suivre visuellement le point sur la trajectoire. L’impression donnée était celle d’une courbe stationnaire fermée lumineuse. Dans un régime stochastique, l’impression visuelle était qu’une surface entière était couverte par le mouvement (en fait cette surface était une projection plane d’un attracteur étrange). Au contraire, autour de valeurs bien définies du paramètre de contrôle, r, une figure intermédiaire était observée : une courbe apparemment fermée était détruite par des bouffées intermittentes : durant ces bouffées, une surface entière était couverte par le point, puis une courbe fermée était reformée et ainsi de suite." 810 ’Cette observation numérique s’accompagne, quelques temps après, de l’observation d’un phénomène apparemment similaire dans les cellules de convection de Rayleigh-Bénard par Libchaber et Maurer, à l’Ecole Normale Supérieure. Pomeau s’engage alors dans la recherche d’un cadre interprétatif et, en 1978, il demande à Manneville (du CEA de Saclay, où ils travaillent tout les deux) de réaliser des calculs sur machines numériques, digitales, afin de retrouver et affiner les résultats obtenus sur machine analogique, dont la précision n’est pas toujours facile à maîtriser. A partir de la confirmation numérique, le processus d’analyse qui conduit à la construction du scénario de l’intermittence 811 , s’engage avec la collaboration de Pomeau et Manneville.
Leur interprétation se construit de manière semi-quantitative, sur la base d’explorations numériques du système de Lorenz, et grâce à une utilisation et une interprétation des mathématiques des systèmes dynamiques.
Le souci de se fonder sur les systèmes dynamiques s’illustre en plusieurs points. En premier lieu il s’exprime dans l’étude de la stabilité structurelle du système de Lorenz, qui est importante puisqu’elle permet d’assurer les raisonnements topologiques développés dans le cadre des systèmes dynamiques. Avec ces physiciens, cette stabilité est caractérisée de manière heuristique : le fait de trouver des comportements similaires pour des évaluations numériques à différentes valeurs des paramètres est un critère, opératoire, suffisant 812 .
Dans la même veine, une première explication qualitative du processus observé est construite sur la base des variétés stables du cycle limite et en considérant que la bifurcation déstabilise l’une d’elles. Le mouvement se compose d’un parcours à proximité du cycle "limite" (qui n’en est plus vraiment un puisque le cycle est légèrement instable). La trajectoire s’écarte donc progressivement de ce "fantôme", suffisamment lentement pour laisser l’impression qu’il s’agit encore d’un cycle limite. Lorsque l’éloignement est assez important il apparaît des bouffées turbulentes, résultat de l’attraction vers la variété instable (qui domine la faible instabilité de cette variété) 813 .
La construction d’une application de premier retour permet de traduire de manière semi-quantitative ce qui se passe. Le choix classique pour étudier le système de Lorenz n’est pas pertinent dans la perspective de leur démonstration ; ils choisissent et construisent la section x=0 (qui est donc bidimensionnelle). Puis ils établissent, avec les données numériques, une application unidimensionnelle en y, suffisamment représentative :
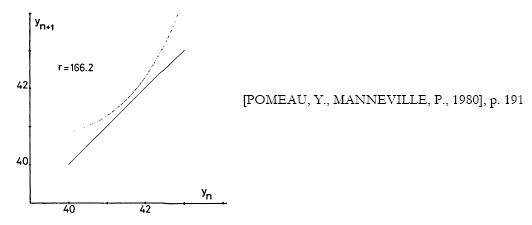
Dans l’interprétation de Pomeau et Manneville, la transition par la voie intermittente correspond au changement de configuration relative de la parabole et de la première bissectrice (voir la figure ci-dessous). Pour r < r T , la parabole coupe la bissectrice en deux points (un stable, l’autre instable) ; à r T , valeur du paramètre à la transition, les deux points fusionnent (la parabole est tangente à la bissectrice et le point de contact correspond à un cycle limite), puis au-delà, r > r T , il se forme un canal entre la parabole et la droite. Le canal correspond a la phase laminaire (à proximité du cycle limite lorsque r=r T ) ; lorsque le point s’écarte du goulot, le comportement devient temporairement apériodique, turbulent, puis lors d’un nouveau passage ultérieur, à proximité du goulot, une nouvelle phase laminaire apparaît.
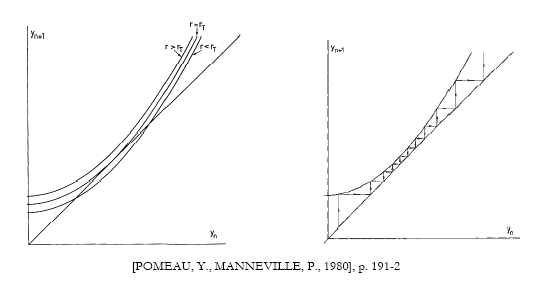
Tels sont les premiers pas théoriques de l’interprétation, qui montre, selon Franceschelli, que "l’invention du scénario d’intermittence a été réalisé petit à petit, à partir de l’exigence de fournir une explication qualitative pour un phénomène observé, c’est-à-dire à partir d’une démarche très phénoménologique et assez peu axiomatique" 814 . Le cadre théorique est étendu par la suite, pour donner la distinction en trois types d’intermittence I, II, III 815 . On peut ajouter que sur le modèle de Lorenz, Pomeau et Manneville estiment 816 que la durée des phases laminaires suit la loi de puissance t~(r-r T ) 1/2 , au voisinage de la transition r T .