Les oscillations non linéaires en Europe occidentale

L’Europe de l’ouest, essentiellement, ne reste pas inactive durant ces quelques années. Comme nous le verrons au chapitre 8 la problématique des oscillations non linéaire occupe une communauté importante dans les années 1930. Il faut signaler que jusqu’en 1937 au moins, les relations scientifiques, sur le thème des oscillations non linéaires, avec l’URSS sont soutenues et les résultats ne connaissent que l’éventuelle frontière de la langue ⁹¹³ . Mais, pour ce qui est des mathématiques des systèmes dynamiques, les résultats sont plus limités et seuls quelques uns ont compté dans le processus que nous décrivons. On notera au préalable que, un peu à la manière de l’école de Gorki, ces considérations émanent des problèmes de physiques et d’ingénieurs, de l’électronique à la radio et au RADAR. Mais il existe une grande différence : les analyses occidentales ont commencé avec très peu de connaissances des travaux de Poincaré, Lyapounov et Birkhoff, ce qui peut paraître paradoxal.

Chronologiquement, Balthasar Van der Pol est le premier à participer au développement des méthodes quantitatives pour les oscillations dites de "relaxation", en combinant des méthodes classiques, tant analytiques que graphiques ⁹¹⁴ , et son travail plus proche des questions techniques, moins mathématique, est plus impressionnant. En 1928, le français Alfred-Marie Liénard a introduit à la fois une généralisation de l’équation de Van der Pol (parfois appelée équation de Liénard) et un procédé géométrique permettant de montrer l’existence de solutions périodiques dans l’équation ⁹¹⁵ .

D’autres scientifiques peuvent être cités pour des interventions ponctuelles, notamment Jules Haag pour les méthodes d’approximation ⁹¹⁶ . On peut ajouter une liste de mathématiciens français, occupés à des questions d’analyse mathématique et s’intéressant aux équations différentielles, de manière déconnectée des questions techniques. Nous avons mentionné Jean Chazy ⁹¹⁷ . Henri Dulac pour son travail sur les cycles limites doit également être signalé ⁹¹⁸ . Arnaud Denjoy, reprenant une question de Poincaré, développe quelques éléments à propos des équations différentielles sur le tore, qui seront repris par Kryloff et Bogoliuboff ⁹¹⁹ .

Cependant, dans l’entre-deux guerres, ces résultats sont limités. Ce sont des pierres apportées à l’édifice, mais dont l’impact a été moins déterminant que celui des soviétiques, excepté les travaux des mathématiciens Levinson (au MIT), Cartwright et Littlewood (tous deux à Cambridge en Grande-Bretagne).

En effet, la mathématicienne Mary Lucy Cartwright (1900-1998) et son collègue John Littlewood ⁹²⁰ produisent des analyses poussées de quelques équations différentielles bien précises, dérivées des équations de Liénard ⁹²¹ . Ils sont investis dans des recherches sur ces équations issues des techniques de la radio, à partir de 1938, en Grande-Bretagne ; comme leurs homologues continentaux, ils entament leurs recherches sans connaissance approfondie des résultats et des méthodes de Poincaré. Outre-atlantique, Norman Levinson ⁹²² s’engage dans une voie plus méthodologique en proposant de généraliser aux systèmes dissipatifs les résultats des théories des transformations du plan dans lui-même, définies par Poincaré (section transverse et application de premier retour) et développées par Birkhoff (mathématicien à Harvard, établissement voisin du MIT ⁹²³ ) dans le cadre des systèmes conservatifs ⁹²⁴  . En 1944, il propose un article dans la veine de la théorie qualitative des équations différentielles "à la Poincaré", fournissant des moyens topologiques d’étude de la dynamique, qui n’a rien à envier aux travaux soviétiques.

En utilisant les méthodes topologiques de Levinson, Cartwright et Littlewood étudient l’équation de Van der Pol avec terme forcé :

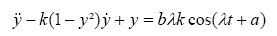
Les résultats publiés en 1945 font état de la découverte, un peu surprenante, d’un ensemble de trajectoires, aux propriétés complexes.

Pour b<2/3 et k assez grand, ils montrent qu’il existe une solution périodique, vers laquelle le comportement tend asymptotiquement. Dans le cas b>2/3, il existe un ensemble K ₀ de trajectoires non périodiques, aux propriétés singulières ⁹²⁵ .

Levinson montre, en 1949, qu’il s’agit bien des "courbes fermées remarquables", dont l’existence avait été soupçonnée dans le cas des transformations analytiques du plan par Birkhoff (et M. Charpentier). Leur présence dans des problèmes de dynamique était douteux ; le travail accompli par les trois mathématiciens l’accrédite et montre en outre que l’objet K ₀ est stable, autrement dit qu’il ne s’agit pas d’un cas trop exceptionnel.

Cartwright, Littlewood et Levinson participent à un mouvement parallèle aux considérations soviétiques et produisent des objets mathématiques étranges. Leur importance sera révélée par les résultats de Smale, quelques années plus tard : en les exprimant dans un langage plus géométrique il en extraira son "fer à cheval".

Dans le domaine des études des équations différentielles, hors d’URSS, il reste à mentionner le travail d’Eberhard Hopf ⁹²⁶ (1902-1983), en matière de théorie des bifurcations. L’histoire a retenu la bifurcation de Hopf (ou Andronov-Hopf) tirée de son principal article publié en la matière en 1942 ⁹²⁷ . Le théorème de Hopf donne un critère pour déterminer quand une famille de points d’équilibre peut bifurquer en une famille de mouvements périodiques, ainsi que l’état de stabilité ou d’instabilité des solutions de la branche bifurquant. Andronov a étudié le même phénomène ; mais de toute manière, Hopf ne prétend même pas innover en la matière et renvoie à Poincaré :

‘"J’ose à peine penser qu’il y a du nouveau dans le théorème ci-dessus. Les méthodes ont été développées par Poincaré il y a peut-être 50 ans et font aujourd’hui partie de la structure conceptuelle classique de la théorie des solutions périodiques […]." ⁹²⁸ ’

A la différence des autres travaux antérieurs à 1945, ces considérations de Hopf ne s’intègrent pas dans une perspective de développement continu d’une problématique, de type étude de la dynamique ou des équations différentielles (elles montrent cependant que les travaux de Poincaré sur les bifurcations ne sont pas totalement ignorés à l’ouest non plus). Hopf se raccroche seulement à Poincaré et le texte est quasiment totalement ignoré avant les années 1970 ⁹²⁹ . Seuls Jürgen Moser y fait allusion en 1964, René Thom dans Stabilité Structurelle et Morphogenèse en 1966 ⁹³⁰ . En reprenant l’interprétation de Aubin ⁹³¹ , c’est le succès de l’article de Ruelle et Takens qui remettra la bifurcation de Hopf au goût du jour. Ainsi on comprend mieux l’hommage rendu à Hopf lors de la conférence de New York de 1977 ⁹³² , qui lui est dédiée.

En définitive, en comparant ces analyses occidentales aux travaux soviétiques, force est de constater qu’ils sont épars, n’ont pas la même cohérence ni la même ampleur théorique. Ils ne sont pas insignifiants, bien au contraire, mais l’école Andronov, en particulier, produit plus que des résultats ponctuels, elle construit un cadre d’étude des oscillations non linéaires.

Avec Birkhoff et Andronov, les systèmes dynamiques sont définis de manière générale comme des équations différentielles : la mention "dynamique" est une référence à la mécanique, à l’évolution déterministe dans le temps. En période de développement des théories probabilistes et de la Mécanique quantique, le terme n’est pas anodin et signe une volonté de se distinguer de ces conceptions. En outre, grâce aux travaux de Birkhoff et d’Andronov, les systèmes dynamiques, autant conservatifs que dissipatifs, trouvent un cadre mathématique bien échafaudé, dont les grandes lignes sont finalement publiées dès 1937. Elles seront mieux diffusées et connues au sortir de la seconde guerre mondiale.

Par ailleurs, le travail de Poincaré trouve toute sa place dans cet ensemble. Ils sont à la base des considérations mathématiques, ils sont intégrés aux deux corpus et avec Birkhoff, rien d’essentiel n’est oublié. Mais, par ce processus, ils ont aussi été étendus, relus, transformés et insérés dans de nouvelles perspectives. Andronov a produit un cadre nouveau et adapté les résultats de Poincaré. Même si le vocabulaire et les outils mathématiques sont repris à Poincaré, l’ouvrage de Birkhoff par la perspective plus topologique adoptée, nous donne à voir les travaux de Poincaré, repensés par Birkhoff, en léger décalage par rapport aux perspectives initiales. L’entre deux guerres est une deuxième étape dans le processus de construction des mathématiques des systèmes dynamiques. La troisième étape, naturellement inspirée par ces développements, profite d’un changement de contexte et de l’action de Solomon Lefschetz.