Le fer à cheval
Smale est parvenu à établir un pont entre ces trois aspects de la dynamique : la dynamique symbolique, le fer à cheval et les orbites homoclines 985 . Rappelons que Birkhoff, s’appuyant sur quelques notions introduites par Hadamard, avait déjà donné une dynamique symbolique pour les structures homoclines 986 . Smale la connaît 987 mais sa construction est beaucoup plus précise que celle de Birkhoff. Surtout, elle rend compte de l’importance de l’étirement-repliement, mécanisme de base du fer à cheval, dans les structures homoclines, avec toutes ses conséquences.
L’application du fer à cheval est l’application qui transforme le carré Q, en ses parties Q1 et Q2 :
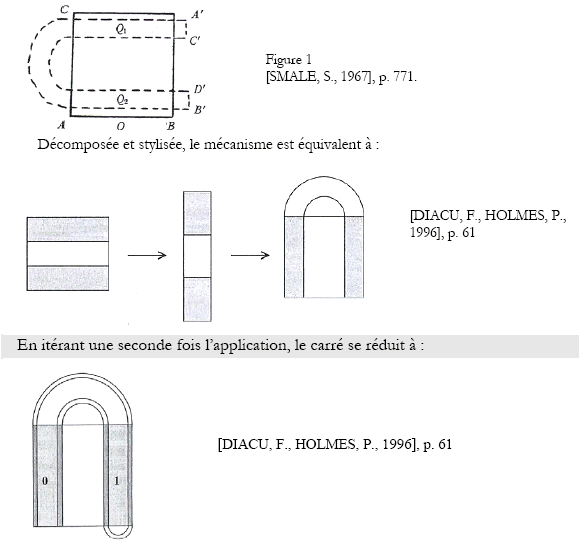
Le lien entre fer à cheval et dynamique symbolique est (relativement) simple à comprendre. Chaque point récurrent par l’itération du fer à cheval (et de son inverse) est adressé par un code, un symbole, constitué par exemple de 0 et de 1. Cela fournit un adressage de l’ensemble des points invariants par l’application, de type ...0, 1, 0 ; 1, 1, 0... :
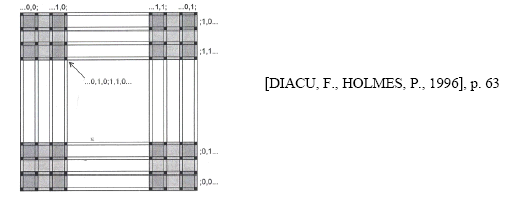
Prenons un point x : si après k itérations du fer à cheval il se trouve dans la bande 0, alors le symbole correspondant à x contient un 0 à la k ième place ; autrement dit k itérations du fer à cheval correspondent à k décalages dans la suite de symboles. Le mécanisme du fer à cheval, dans le système symbolique, est l’"équivalent" d’un décalage dans la suite de symboles.
Tous les points sont repérés par ce système et ce qui est aussi important, des propriétés obtenues sur les séquences symboliques peuvent se transférer en des propriétés de l’application fer à cheval. La dynamique symbolique étant plus simple à gérer et par ailleurs déjà bien étudiée sous des aspects de statistique et de théorie ergodique 988 , c’est un avantage non négligeable.
Pour parvenir un cran plus loin, il faut constater l’analogie graphique entre le schéma d’une courbe homocline et le fer à cheval :
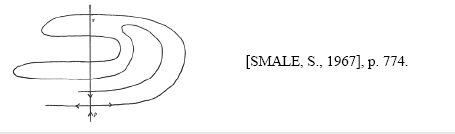
Selon les mots de Smale :
‘"C’est le même phénomène que celui de la Figure 1 [voir ci-dessus, p. 369], mais vu de manière différente. […] L’approche du fer à cheval de la Figure 1 présente un grand avantage au sens où on obtient une image satisfaisante de la structure et de la stabilité des orbites tandis qu’un point homocline donné défie l’analyse à première vue. Telle est l’idée cachée derrière le théorème." 989 ’Le théorème peut s’écrire ainsi :
Soit x un point homocline transverse d’un difféomorphisme f . Alors il existe un ensemble de Cantor Λ ( x étant dans Λ ) et m , nombre entier, tels que f m (Λ)=Λ et f m restreint à Λ est topologiquement un automorphisme de décalage.
Il a un corollaire 990 : dans tout voisinage d’un point homocline transverse, il y a un point périodique.
La description des points homoclines qui défiait l’analyse, se précise et devient l’analogue d’une application fer à cheval et d’un automorphisme de décalage. Ce travail de Smale n’est qu’une facette de son étude des systèmes dynamiques, mais elle est celle qui percera de manière remarquable dans les conceptions de ses successeurs, hors des mathématiques aussi abstraites et malgré le caractère très pointu des outils employés.