b. David Ruelle, les systèmes dynamiques et l’IHES

David Ruelle est membre de l’IHES depuis 1963, l’année de l’arrivée de Thom. Il est mathématicien-physicien d’origine belge et a travaillé dans le domaine de la théorie quantique des champs et de la physique statistique avant d’en venir à l’étude des systèmes dynamiques, quelques temps après son entrée à l’IHES. Depuis 1968 au moins, il réfléchit et essaye "de regarder des problèmes d’hydrodynamique ou, plus généralement, de "phénomènes dissipatifs" d’un point de vue physique analogue à celui de Thom" ¹⁰²⁶ . Sa collaboration avec Floris Takens à l’IHES aboutira à un article d’une grande importance, "On the nature of turbulence" en 1971, donnant une théorie mathématique de la turbulence.

Ce travail mûrit au carrefour de la dynamique topologique et de la "topologie appliquée", dans le contexte de l’IHES. Il prélude à l’utilisation d’une partie des mathématiques des systèmes dynamiques dans l’ère du chaos.

Dans leur article, la turbulence est analysée sur un mode atypique, faisant usage de la théorie des systèmes dynamiques dont on a vu le plein développement à l’IHES à la fin des années 1960. Au sujet de l’apparition de la turbulence, il existait alors deux théories principales : le modèle quasi périodique et celle de Jean Leray ¹⁰²⁷ , datant des années 1930. La seconde s’inscrit dans une perspective de théorie des équations.

En étudiant les équations de Navier-Stokes, Leray a choisi d’associer la turbulence à un phénomène de rupture dans ces équations ; il suppose, en effet, que les équations cessent de décrire le fluide à partir d’une valeur critique et doivent être remplacées par une équation intégrale. Les solutions irrégulières de cette équation forment les solutions turbulentes.

La première, totalement différente de celle de Leray, est due au physicien Lev Landau (1908-1968), publié en 1944 ¹⁰²⁸ , et, indépendamment de Eberhard Hopf, entre 1942 et 1948 ¹⁰²⁹ . Dans ce cadre théorique, la turbulence, le désordre, est le résultat de l’accumulation d’un nombre théoriquement infini de modes d’oscillations, autrement dit d’un mouvement quasi-périodique de plus en plus compliqué, l’accumulation suit l’augmentation progressive du nombre de Reynolds. Chez Landau peu d’arguments précis étayent un tel scénario, excepté des considérations très générales sur la stabilité des solutions.

Avec Hopf, la démarche est beaucoup plus mathématique et s’appuie sur la notion de bifurcation (appelée aujourd’hui bifurcation de Hopf), étudiée en 1942. En substance, il s’agit du même scénario que celui de Landau, exprimé en des termes de mathématiques des systèmes dynamiques.

Comme Ruelle et Takens plus tard, il choisit de paramétrer les équations de Navier-Stokes par une variable µ et d’étudier le comportement des solutions en fonction de µ. Pour µ grand dans son paramétrage, Hopf affirme que le flot laminaire (solution stationnaire) est la seule solution possible ¹⁰³⁰ . Puis, à différents seuils, µ ₀ , µ ₁ , µ ₂ ..., Hopf conjecture que le système subit une série de bifurcations (de Hopf) infinie et que le système évolue dans une variété M(µ) : par exemple, après la première bifurcation, M(µ ₀ ) est un cycle limite de Poincaré.

Lorsque Ruelle et Takens interviennent, la théorie dominante dans la communauté des physiciens est celle de Lev Landau. L’analyse de Ruelle et Takens vise à critiquer cette théorie et propose une théorie alternative ¹⁰³¹ . Leur démarche est à la fois similaire à celle de Hopf ¹⁰³² , dans le sens où il s’agit d’une analyse en termes dynamiques (et non statistiques) et construite sur des mathématiques de même type, et très innovante, parce qu’ils ont recours à des procédés mathématiques extrêmement poussés et abstraits : la topologie et son utilisation pour la modélisation, telle que Thom en a démontré l’utilité, les notions de généricité et de stabilité structurelle.

Quelques citations suffisent à remettre l’article dans ce contexte. Les deux lignes de remerciements sont très claires :

‘"Les auteurs remercient avec plaisir R. Thom pour les discussions de grande valeur […] L’ouvrage de Thom [12] (à paraître) a été une source d’inspirations pour le présent article" ¹⁰³³ ’

Dans son ouvrage de réflexion de 1991, Ruelle rappelle :

‘"La description de la turbulence en termes de modes par Landau m’a tout de suite déplu parce qu’elle était en désaccord avec des idées mathématiques que j’avais entendu exposer (sic) par René Thom, et que j’avais étudiées dans un article fondamental de Steve Smale sur les systèmes dynamiques différentiables. Le Français René Thom et l’Américain Steve Smale sont tous deux d’éminents mathématiciens [...] C’est d’eux que j’ai appris les développements modernes des idées de Poincaré sur les systèmes dynamiques, et à partir de là il était clair que le paradigme des modes est loin d’être universellement applicable." ¹⁰³⁴ ’

L’idée générale pour l’apparition de la turbulence est la suivante : au bout d’un petit nombre de bifurcations il se crée un attracteur dit "étrange" (représentant la turbulence) et le scénario est générique. L’analyse de l’article fait ressortir les principales connexions conceptuelles, au-delà de la mention de la notion d’attracteur et généricité.

Dans leur article, ils considèrent les équations de Navier-Stokes, comme système dynamique à un paramètre µ, sans se préoccuper de la forme exacte des équations :

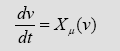
Partant de l’état de repos (µ=0), le régime du fluide passe à un état stationnaire pour µ faible (un point fixe dans l’espace des phases). Par le franchissement d’un seuil µ ₁ , le champ de vitesse subit une bifurcation d e Hopf ¹⁰³⁵ et génère un état d’oscillation de fréquence ω ₁ .

A une seconde valeur critique µ ₂ , une autre bifurcation de Hopf crée un régime d’oscillation de fréquence ω ₂ , indépendant du précédent et s’y superposant. Il s’agit en quelque sorte d’une preuve mathématique de ce que Hopf avait imaginé.

Si µ augmente encore, alors le "mouvement du fluide devient très compliqué, irrégulier et chaotique, nous avons de la turbulence" ¹⁰³⁶ . Mais pour cela, il n’est nul besoin d’attendre le franchissement de multiples paliers ω _n  : un nombre limité (3 ou 4) suffit. Le scénario de Landau et Lifschitz ¹⁰³⁷ correspond en fait à un grand nombre de paliers ω _n . L’article de Ruelle-Takensprouve mathématiquement que ce scénario n’est pas générique ¹⁰³⁸ et n’a donc que très peu de chance d’être observé en pratique. Sur cet exemple, les outils des systèmes dynamiques montrent qu’ils peuvent être remarquablement utiles.

Ruelle et Takens s’inspirent notamment de l’article de Smale de 1967, dont l’essentiel était de traiter des systèmes dynamiques de dimension supérieure à deux, comme dans le cas présent. La notion d’attracteur "étrange", définie comme le produit d’un ensemble de Cantor par une variété, est inspiré du fer à cheval et des constructions de Smale. Un attracteur étrange tel qu’il est présenté dans l’article, est stable, ce qui fait qu’il "ne peut pas être rejeté comme une pathologie non générique" ¹⁰³⁹ . En 1971, leur caractérisation de la turbulence s’arrête à ces grandes lignes à la fois qualitatives et extrêmement pointues.

L’article de 1971 a ainsi hérité des analyses de Thom et Smale, des analyses topologiques "appliquées" de Thom, de la théorie des systèmes dynamiques développée dans le contexte de l’IHES. En outre, il signe une rencontre entre ces théories mathématiques abstraites et la physique, selon une perspective qualitative, peu habituelle en physique. L’optique de Ruelle et Takens est atypique dans le sens où ils ne considèrent pas les équations d’un système donné, ne s’embarrassent pas des détails d’un modèle précis. Au contraire, pour reprendre la formule d’Aubin, ils arrêtent de regarder des représentations spécifiques de la nature pour étudier les conséquences du mode de représentation lui-même ¹⁰⁴⁰ .

Ce résultat va connaître un tout autre sort que la théorie des catastrophes. Dans ses démarches, Ruelle fait preuve de beaucoup d’ouverture, contrairement à Thom. Ici, l’arrogance mathématique laisse la place à plus de diplomatie dans les contacts avec des hydrodynamiciens qui se montrent d’abord peu enthousiastes avant d’adhérer un peu plus largement aux thèses de Ruelle. Il est difficile d’admettre qu’une analyse mathématique puisse suggérer de chercher des alternatives aux théories physiques, mais c’est tout le sens de l’opération de Ruelle lorsqu’il prend contact avec des expérimentateurs. Cette approche participera du véritable succès de l’entreprise et du développement considérable des notions d’attracteur étrange, de turbulence et de chaos.

En outre, la teneur mathématique du travail de 1971 ne doit pas faire oublier que Ruelle est aussi un physicien, théoricien. La turbulence est un phénomène physique, hydrodynamique et l’ouverture vers les expérimentateurs traduit une volonté d’éclaircir cet aspect du problème. La caractéristique de son travail est de mettre les mathématiques au service d’objectifs théoriques : par l’utilisation d’une forme de modélisation à la Thom d’une part, et par une formalisation très poussée des problèmes d’autre part. Outre l’article de 1971 qui illustre bien ceci, il faut mentionner ses travaux de Mécanique statistique, remarquables au point de vue théorique. Ainsi, dans l’introduction de son traité de 1969, il exprime sa vision des mathématiques dans la physique :

‘"L’analyse mathématique donne au monde physique une nouvelle structure et un nouveau sens. La connaissance de cette structure et de ce sens constitue une intelligibilité de la ‘nature des choses’ aussi profonde que l’on peut espérer. […] Le progrès de la physique mathématique pourrait être promu significativement, selon l’opinion de l’auteur, par la disponibilité de résultats d’importantes théories mathématiques sous des formes concises et sans preuves, dans l’esprit des ‘Fascicules de Résultats’ de Bourbaki." ¹⁰⁴¹ ’

Il faut donc lire les résultats de 1971 à la lumière de cette volonté de rigueur mathématique, de référence à Bourbaki et d’une attitude structuraliste qui marquent le travail de Ruelle ¹⁰⁴² , en turbulence comme en Mécanique statistique. Le chapitre suivant nous montrera l’autre versant, celui de la Mécanique statistique et l’ergodicité à l’oeuvre dans les travaux de Ruelle.