La rencontre de deux traditions

Chronologiquement, même s’il a été publié après celui de Birkhoff, Von Neumann  est l’auteur du premier théorème ergodique ¹⁰⁵⁰ . Vers la fin de l’année 1931, les deux résultats sont prêts. Birkhoff fait paraître son résultat en deux articles consécutifs (datés du 27 novembre et du 1er décembre 1931) ¹⁰⁵¹  ; celui de Von Neumann est publié en janvier 1932 ¹⁰⁵² , dans la même revue. Ces deux résultats fondamentaux sont le fruit d’une seule et même rencontre entre deux traditions incarnées par Von Neumann et Birkhoff.

En effet, jusqu’à cette époque, Von Neumann est préoccupé par les questions de la Mécanique quantique et son intérêt pour la Mécanique statistique, et la thermodynamique, leur est fortement associé. Il est manifestement inspiré par la lecture de l’article des Ehrenfest ¹⁰⁵³ comme son résultat le reflète.  En substance, Von Neumann utilise des méthodes d’opérateurs sur les espaces de Hilbert, pour parvenir à montrer que la moyenne temporelle existe "en moyenne L₂" ¹⁰⁵⁴ , comme son précédent travail de 1929 ¹⁰⁵⁵ . En outre, il donne une condition pour que le système soit "ergodique", c’est-à-dire que la moyenne temporelle égale la moyenne spatiale : tout ensemble invariant dans la dynamique est soit 0, soit l’espace des phases entier (le sous-espace d’énergie donnée pour être plus précis). Le théorème de Von Neumann est inscrit dans une histoire bien délimitée, qu’on pourrait même qualifiée d’"européenne" ¹⁰⁵⁶ .

De son côté, Birkhoff est plus intéressé par la Mécanique classique, les systèmes dynamiques et Poincaré. Son théorème ergodique s’adosse à ses propres considérations sur les systèmes dynamiques ¹⁰⁵⁷ . Il montre d’abord un résultat de récurrence, avec l’hypothèse de "transitivité forte" ¹⁰⁵⁸ , qui correspond au fait que "tout ensemble mesurable de trajectoires complètes dans M est de mesure 0 ou V, où V est le volume total de M" ¹⁰⁵⁹ . Le théorème de récurrence de Poincaré ¹⁰⁶⁰ , la question des sections transverses ¹⁰⁶¹ , la notion de mouvement récurrent forment l’arrière-plan de son résultat. Le titre du premier article du 27 novembre 1931 suffit à faire ressortir clairement sa perspective : "Proof of a recurrence theorem for strongly transitive dynamical systems".

Dans la seconde partie des articles, Birkhoff prouve son "théorème ergodique", valable sans hypothèse de transitivité forte : "il existe une ‘probabilité de temps’ p bien définie selon laquelle tout point se déplaçant sera dans une région v, sauf pour un ensemble de mesure 0 ;" ¹⁰⁶² , c’est-à-dire que la limite :

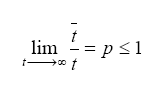
Malgré les différences dans leur apparence, les deux théorèmes sont le résultat du croisement de ces deux perspectives de recherches. Birkhoff s’inspire de Von Neumann ¹⁰⁶³ et inversement, Von Neumann a utilisé un résultat de Bernard Osgood Koopman (1900-1981) ¹⁰⁶⁴ , un élève de Birkhoff. Dans son travail sur les systèmes dynamiques ¹⁰⁶⁵ , Koopman est parvenu à établir un lien entre les systèmes dynamiques et les transformations des espaces de Hilbert ¹⁰⁶⁶  : ce résultat constitue en quelque sorte la trace mathématique de la rencontre des deux traditions mises en avant.

Dans la confrontation avec le théorème de Von Neumann, la perspective adoptée par Birkhoff sur son théorème ergodique va légèrement évoluer, d’une manière finalement assez peu inattendue et très significative.