Le modèle de Hénon-Heiles

Une toute autre série de calculs numériques, engagée à l’initiative de l’astronome français Michel Hénon (né en 1933) va conduire à une surprise équivalente. Hénon s’intéresse à la dynamique des amas globulaires, sujet sur lequel il a produit une thèse achevée en 1961 ¹¹⁸⁷ . L’année suivante il est invité au Princeton University Observatory, où il s’intéresse à un autre problème de dynamique : celui du mouvement d’une étoile dans une galaxie axisymétrique et le problème de la "troisième intégrale" dans ce modèle.

Divers travaux numériques laissaient alors augurer de l’existence d’une telle intégrale, mais avec ses propres simulations numériques Hénon observait un comportement plutôt erratique des trajectoires, difficile à croire et contraire à l’idée qu’une intégrale existe dans toutes les configurations du modèle. Encadrant un étudiant de Princeton, Carl Heiles, les calculs sont refaits et ce surprenant résultat est confirmé ¹¹⁸⁸ . Ces observations sont répercutées dans leur article "The applicability of the third integral of motion", daté de 1964 ¹¹⁸⁹ .

Les motivations de ces recherches diffèrent de celles des expériences FPU. Dans une perspective proche de la Mécanique céleste et des systèmes dynamiques selon Poincaré et Birkhoff, Hénon s’intéresse aux systèmes dynamiques conservatifs dans leurs aspects numériques ; il n’est pas autant aguerri aux notions d’ergodicité. L’analyse produite dans le texte de 1964 reflète ces deux tendances. D’un côté, l’analyse est conduite dans une surface de section, bidimensionnelle, de l’espace des phases. La simple observation des comportements calculés conduit alors à distinguer deux types : les trajectoires qui s’alignent sur des courbes fermées et celles qui évoluent entre les courbes fermées ; ces dernières sont appelées "ergodiques" puisqu’elles tendent à couvrir l’espace entre les courbes. De l’autre, les analyses des comportements "ergodiques" sont assez limitées et très opératoires.

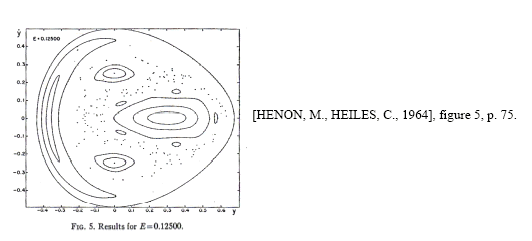
Précisons les aspects problématiques des observations. Lorsqu’il existe une intégrale, le mouvement s’agence sur des courbes fermées : les expériences montrent donc que l’existence d’une intégrale n’est pas générale. De plus, la quantité de courbes "ergodiques" dépend des paramètres du modèle (l’énergie totale, en l’occurrence) et il existe une transition progressive des systèmes où seules des courbes fermées existent, vers des systèmes où les trajectoires "ergodiques" occupent tout l’espace. Pour préciser la transition, les deux comportements sont distingués grâce à un critère assez empirique construit sur le constat suivant : sur les courbes fermées, deux points initialement proches s’écartent très lentement, alors que pour une trajectoire "ergodique" l’écart croît "grossièrement exponentiellement" ¹¹⁹⁰ .

La coïncidence avec les propositions courantes chez les scientifiques soviétiques est très remarquable, mais il s’agit ici avant tout d’un critère opératoire et commode. Hénon ignore encore les théories proposées en Union Soviétique.

Peut-être faut-il néanmoins rapprocher ce choix des travaux de J. Moser (le M de KAM) : Hénon a assisté, en décembre 1962, à une conférence d’astronomie où Moser est intervenu pour présenter ses résultats (le théorème KAM en l’occurrence) et ses enjeux. Il est concevable que Hénon a pu en extraire du sens pour son résultat et une explication de ce mélange d’ordre et de désordre si troublant pour la communauté des astronomes ¹¹⁹¹ .

En tout cas, les résultats remettent en question la dichotomie déjà critiquée par Kolmogorov, entre les modèles intégrables "simples" et les non intégrables, "ergodiques". Très symboliquement, on peut ajouter que le problème restreint des trois corps fait partie des systèmes concernés par ce mélange de comportements, comme Poincaré et Birkhoff l’avaient pressenti.

Par la suite, Hénon ne s’intéresse pas davantage aux propriétés statistiques et reste très attaché aux questions de la Mécanique céleste. En revanche, tout comme l’expérience FPU, le modèle intéressera les physiciens préoccupés par la physique statistique et servira les tentatives pour repenser l’ergodicité. Le texte de Benettin et ses collaborateurs, en 1976, en est une illustration parmi d’autres ¹¹⁹² .

Il convient d’ajouter cependant qu’un seul mathématicien s’est intéressé très tôt au problème suscité par ces expériences numériques : Vladimir Arnold. Il est vrai qu’il est un des mieux placés pour en comprendre tout l’enjeu. C’est également une preuve de la réceptivité d’un mathématicien-physicien habitué à l’interaction avec les problématiques proches de la physique ¹¹⁹³ .