b. Vers les oscillations de relaxation de Van der Pol
Les travaux de Balthasar Van der Pol (1889-1959) sont décisifs dans la mutation des années 1930. Il s’est fait une spécialité des analyses des dispositifs électroniques de la radio. Il a été formé à la physique à l’université d’Utrecht, a passé deux années à Cambridge chez J.J. Thomson, puis est retourné en Hollande, chez H.A. Lorentz. En 1920 il achève sa thèse sur la propagation des ondes radio dans un gaz ionisé, réalisée sur la base d’expériences faites à Cambridge 1235 . Il est embauché chez Philips en 1922, où il fait le reste de sa carrière et mène des recherches pour lesquelles il aime à mêler le travail de conception de l’ingénieur, du physicien et du mathématicien.
Dès 1920 il s’engage (avec E. Appleton) dans une "théorie non linéaire générale" 1236 pour les générateurs à triode, analysant les propriétés de stabilité des oscillations et leurs conditions de production, combinant les développements approchés aux résolutions graphiques. Son analyse de 1926 va induire l’idée d’un mécanisme général des "oscillations de relaxation" lui permettant de multiplier les analogies et de proposer une pratique nouvelle. Le cadre de l’analyse harmonique est dépassé à tous les niveaux.
Au départ, en 1926, il s’agit d’étudier l’équation d’oscillation d’un circuit à triode 1237 :
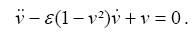
Dans les conditions habituelles d’expérimentation le paramètre correspond à ε<<1 ; Van der Pol cherche ce qui peut se passer pour ε>>1. Par les mathématiques il s’engage en quelque sorte à faire cette expérience, qu’il n’envisage pas, dans un premier temps, de réaliser électroniquement. Il ne parvient qu’à établir des solutions graphiques, dont voici le premier exemplaire :
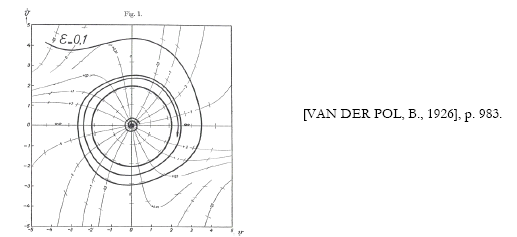
Bien que Van der Pol connaisse une partie des travaux de Poincaré 1238 , il ne fait pas le rapprochement avec un cycle limite de Poincaré. Par une analyse qualitative de la physique du phénomène, il explique le comportement oscillant : celui-ci a une période qui décroît asymptotiquement, comme un phénomène de relaxation, et il est baptisé "oscillation de relaxation".
La notion d’oscillation de relaxation, en 1926, est directement liée à l’équation qu’il considère comme "l’équation générale pour les oscillations de relaxation" 1239 . C’est ce qui l’engage à rechercher des phénomènes électriques soumis à la même équation, ce qu’il juge facile à faire : il reprend le multivibrateur d’Abraham et Bloch, construit un second dispositif et imagine déjà que les oscillations des tubes néons pourront rentrer dans cette catégorie 1240 .
Rapidement, dans l’esprit de Van der Pol, les oscillations de relaxation ont une certaine généralité. En 1930, invité à une conférence à Paris 1241 , Van der Pol fait un rapide inventaire montrant l’importance de ces oscillations. Il y affirme :
‘"Une oscillation de relaxation a lieu, d’une manière générale, toutes les fois qu’un mécanisme, contenant une source d’énergie continue, permet à un phénomène essentiellement apériodique de se répéter automatiquement un nombre infini de fois. Un grand nombre de phénomènes des plus familiers rentrent dans ce schéma, par exemple : le grattement d’un couteau sur une assiette, le grincement d’un tiroir ou d’une porte, la claquement d’un drapeau, le chant d’une bouilloire, d’un tuyau de distribution d’eau, la ligne pointillée qu’on peut faire à la craie sur un tableau noir...etc." 1242 ’Van der Pol propose beaucoup d’analogies. Elles reposent sur deux éléments : un mécanisme général et l’indépendance des modèles mathématiques par rapport au support matériel des oscillations. En conclusion de son intervention, il résume son projet :
‘"J’espère avoir ainsi montré comment l’étude des principes mathématiques qui gouvernent un mode de fonctionnement très général dans la nature, conduit à relier entre eux un grand nombre de phénomènes particuliers qui paraissent, à première vue, étranger les uns aux autres" 1243 ’En réalité, Van der Pol suggère des rapprochements plus qu’il n’approfondit ces relations, mais il donne un exemple particulièrement détaillé : le battement du coeur. En effet, il publie en 1928, avec J. Van der Mark, un article sur "Le battement du coeur considéré comme oscillation de relaxation et un modèle électrique du coeur" 1244 . Le "modèle électrique du coeur" est un système de trois circuits de relaxation couplés, représentant trois parties du coeur : sinus, oreillette et ventricule. Le dispositif permet de simuler des électrocardiogrammes, et d’imaginer des anomalies dans le rythme cardiaque.
La démarche est particulièrement intéressante : on ne s’intéresse qu’aux oscillations du système, pas au fonctionnement biologique du coeur et le modèle électrique n’a pas prétention à représenter le mécanisme cardiaque, mais seulement à l’imiter. L’analogie porte sur la dynamique des systèmes cardiaques / électriques laquelle est sous-tendue par l’équation mathématique des oscillations de relaxation.
Pour Giorgio Israël, Van der Pol témoigne de conceptions modélistes nouvelles, en construisant un modèle sous forme d’analogie mathématique. Nous pensons avec lui, que Van der Pol fait abstraction du mécanisme biologique et qu’il modélise le coeur comme un ensemble d’équations de relaxations, permettant de reproduire ses comportements. Mais si Israël s’intéresse surtout à la question de la modélisation, nous ne pouvons pas considérer ici que la modélisation soit une fin en soi. En effet, il ne faut pas perdre de vue que la simulation est l’objectif premier et que l’analogie est construite avec l’espoir d’imiter la dynamique du coeur. En 1960, dans sa courte biographie de Van der Pol, le physicien Hendrik Casimir affirmait :
‘"Avec Van der Mark, il a conçu un circuit dont les oscillations imitent au plus près un électrocardiogramme […] Ce travail, outre qu’il montre l’intérêt de Van der Pol pour la médecine, fournit un exemple d’une tendance qui est présente à travers tout son travail : la tendance à chercher des phénomènes différents qui sont décrits par les mêmes équations. Cette façon de pensée conduit souvent à des ‘ordinateurs analogiques’ pratiques." 1245 ’Casimir pointe une originalité de l’approche de Van der Pol : la pratique de l’analogie, si elle constitue une démarche générale chez Van der Pol, ne doit pas être déconnectée des possibilités de conduire au calcul et à la simulation. Van der Pol le signifie particulièrement bien dans la conférence de 1930. En comparant les relevés expérimentaux de trois évolutions dynamiques, le régime permanent d’une triode, une population de drosophiles et la croissance d’un tournesol, il conclut :
‘"La ressemblance intime de ces phénomènes, physiquement si dissemblables, mais mathématiquement analogues, ne saurait être niée. Il est donc très vraisemblable que des problèmes de population plus compliqués, dont la solution analytique serait difficile à obtenir (nous en verrons d’autres exemples par la suite) pourront être résolus expérimentalement en laboratoire à l’aide des oscillations des lampes triodes. Car dès que nous sommes assurés que nos équations représentent correctement un certain problème de population, il est le plus souvent assez simple d’établir un réseau électrique comprenant des lampes et satisfaisant à ces équations, et comme il est beaucoup plus facile d’expérimenter avec des courants électriques qu’avec la matière inerte (sans parler de la matière vivante) la méthode électrique suggérée ci-dessus peut être utilisée avec avantage." 1246 ’Cette citation souligne le renversement épistémologique, parfaitement assumé par Van der Pol, réalisé grâce à l’analogie mathématique et à l’analogie avec les circuits électroniques. A propos du battement du coeur, on peut donc voir la démarche de Van der Pol comme la construction d’un modèle mathématique, il nous paraît plus intéressant de le comprendre comme un "modèle électrique" et la réalisation d’une simulation analogique du coeur reposant sur une analogie mathématique.
En tout cas, par ces analogies mathématico-électriques, Van der Pol complète sa théorie non linéaire mathématique un peu rudimentaire et il donne les moyens d’analyse des dynamiques non linéaires et des oscillations de différents phénomènes naturels. C’est la meilleure expression de l’alchimie entre physique, mathématique et ingénierie électrique produite par Van der Pol.
Van der Pol n’a jamais recours à l’oscillateur harmonique et n’envisage même pas d’établir un spectre de Fourier de l’oscillation. Ceci illustre une prise de conscience du fait que les phénomènes non linéaires ne peuvent pas être correctement expliqués par ces outils typiques du linéaire, ainsi que son analyse mathématique l’a montré. Pour mieux signifier le changement, il nous paraît pertinent d’affirmer que dans l’esprit de Van der Pol l’oscillation de relaxation joue, pour les oscillations non linéaires, le rôle que l’oscillateur harmonique a dans la théorie linéaire.
Van der Pol introduit donc une pratique de l’analogie dans l’étude des oscillations. Le parallèle avec Otto Rössler nous paraît facile à faire, même si de multiples développements en théorie des oscillations le séparent de Van der Pol. En outre, le calcul analogique électronique n’en est qu’à ses balbutiements dans les années 1930 et la démarche de Van der Pol reste limitée par le développement technique.
Absentes des travaux de Van der Pol, les méthodes de Poincaré intègrent l’étude des oscillations durant le plein développement des oscillations de relaxation. Ce moment est associé, au départ, à des questions de physique : il s’agit des travaux de l’école d’Andronov, dont nous n’aborderons pas les aspects relatifs à la modélisation, renvoyant pour cela à au chapitre 6.