a. La figure des planètes et les formes de bifurcation
A côté des grandes réflexions sur le problème des trois corps, Poincaré se penche sur un autre sujet de Mécanique céleste, la figure des planètes. Les astronomes cherchaient à expliquer la formation des planètes en supposant qu’elles étaient constituées initialement comme des masses fluides en rotation soumises à leur propre potentiel de gravitation F. Plusieurs questions controversées sont associées à ce problème, notamment la formation de la Lune et l’origine de l’Univers 1868 . Poincaré ne participe pas directement à ces controverses mais balise le terrain de quelques réflexions mathématiques.
Au cours de l’année 1885, Poincaré écrit ses premières notes à ce sujet, destinées à débattre des résultats nouveaux décrits dans le Treatise on Natural Philosophy 1869 de Tait et Thomson, "sans aucune démonstration" 1870 . Ceux-ci avaient annoncé des nouvelles formes possibles pour l’équilibre des masses fluides en rotation, s’ajoutant aux formes déjà connues : les formes sphéroïdales, l’ellipsoïde de Maclaurin (ellipsoïde de révolution aplati) et l’ellipsoïde de Jacobi (trois axes inégaux). La démarche de Poincaré est tout à fait analogue à la démarche globale et qualitative élaborée au sujet des équations différentielles et à l’ensemble de leurs solutions. Comme le fait remarquer Hadamard :
‘"[…] on se convaincra que tous les progrès réalisés par Poincaré sur cette question sont dus à ce qu’il n’envisage pas une figure d’équilibre, un ellipsoïde de Maclaurin ou de Jacobi déterminé, en elle-même, mais bien dans ses relations avec les figures d’équilibre voisines" 1871 ’Ainsi Poincaré est-t-il amené à introduire la notion d’équilibre de bifurcation (ou forme de bifurcation, ou bifurcation, selon les textes) qui sont des points d’où émergent des nouvelles formes, à partir des ellipsoïdes connus. Les premiers résultats de Poincaré, en 1885, se résument ainsi :
‘"Les formes d’équilibre du système considéré sont données par les équations [F est le potentiel gravitationnel]:’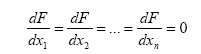
Autrement dit, les ellipsoïdes de Maclaurin et de Jacobi appartiennent à deux séries linéaires et peuvent se rencontrer à une forme de bifurcation, qui est, par définition, en même temps un ellipsoïde de Maclaurin et de Jacobi.
Le second problème posé par les figures d’équilibre est leur stabilité. Les coefficients de stabilité, une série finie de termes, servent à caractériser cet équilibre. Ils permettent de préciser le minimum du potentiel F (les coefficients renvoient à la décomposition en carré d’une certaine forme quadratique). La condition de stabilité correspond la positivité de tous les coefficients. L’annulation d’un seul coefficient renvoie alors à une forme de bifurcation. En suivant une série linéaire et l’évolution des coefficients, lorsqu’on aboutit à un coefficient nul, on reconnaîtra qu’il existe une autre série à laquelle la forme de bifurcation appartient.
En outre, il se produit un phénomène d’échange de stabilité au niveau des bifurcations. Si sur l’une des deux séries se rejoignant il ne se trouve que des figures stables, alors, après la bifurcation, toutes les figures seront instables : les figures stables passeront dans l’autre série.
Cette recherche des formes d’équilibre est entreprise également par A. Lyapounov, par ailleurs théoricien des mathématiques de la stabilité, dont l’importance apparaît au cours du XXème siècle. Il ne s’agit plus de question de bifurcation mais de notions de stabilités et de formes particulières que Lyapounov met en évidence au fil de ses travaux 1873 . Poincaré, dès 1887 1874 , a connaissance de ces travaux. Il signale d’ailleurs que parmi les recherches inspirées par Thomson et Tait "les plus importantes sont, sans contredit, celles de M. Liapounoff" 1875 . Plus que les résultats de Lyapounov, c’est le rapprochement des problématiques de Poincaré et Lyapounov autour de la stabilité qui est intéressant.
Le dernier sujet à mettre en avant, dans la perspective "cosmogonique" de ces réflexions mathématiques, est la question des anneaux de Saturne. Elle ne serait qu’une anecdote dans les travaux de Poincaré si, autour de ce thème, ne s’étaient développées plusieurs réflexions, dont celles de J.C. Maxwell (1855) 1876 . La constitution des anneaux et leur stabilité font problèmes : sont-ils solides ou fluides ? sont-ils constitués d’un grand nombre de masses ? 1877 D’une part Maxwell a participé aux réflexions de type masse fluide en rotation. D’autre part, et c’est peut-être plus important, ce problème lui a donné l’idée de sa méthode "statistique" et de son application aux phénomènes reposant sur un grand nombre de masse en interactions 1878 .