La ramification vasculaire (1926-1927)

Avant tout, nous nous devons de produire un avertissement. Dans ce paragraphe, comme dans ceux qui suivront, nous ne traiterons bien sûr pas des premières approches mathématisées du système sanguin en général mais seulement des premières approches mathématisées qui ont été en même temps centrées sur la forme visible, sur la structure spatiale ramifiée de ce système. S’il fallait se livrer à une restitution des approches mathématisées en général, notre historique se confondrait quasiment avec une histoire des physiologies physique et chimique dans leur ensemble. Ce qui n’est ni notre objet, ni notre ambition puisque nous désirons simplement pouvoir, à terme, comprendre comment se sont positionnés les travaux de modélisation et de simulation de la forme et de la croissance des plantes dans des travaux concurrents ou plus anciens, et principalement fondés sur des théorisations mathématisées et des modélisations mathématiques.

Aussi, rappelons ici brièvement et simplement pour mémoire que des études mathématisées sur la circulation sanguine, basées sur des modèles physiques analogues, avaient été déjà produites par Leonhardt Euler (1707-1783) dès 1762 ²²⁶ . Significativement, Euler y avait essentiellement étudié le dimensionnement du système de circulation sanguine mais pas sa forme ni sa configuration spatiale précise. À l’aide d’une formalisation de type mécaniste, Euler se représentait en effet le système circulatoire de façon simplifiée comme un réservoir élastique muni d’une résistance périphérique et d’une pompe ²²⁷ . Comme on le voit, les ramifications n’y avaient pas été considérées.

Dans ce domaine de représentation mathématisée de la vascularisation, les travaux fondateurs de Cecil D. Murray ont, pour leur part, été publiés dès 1926 dans les Proceedings of the National Academy of Sciences, à Washington ²²⁸ . Indépendamment de l’approche finalement globale et assez qualitative de d’Arcy Thompson, car n’allant jamais jusqu’à la quantification des lois, les recherches quantitatives dans lesquelles s’insèrent les travaux de Murray, et que nous allons évoquer, étaient au contraire nées, dans les milieux de la physiologie médicale, de considérations plutôt concrètes et à visées utilitaires. Ces travaux quantitatifs axés sur la mise en place de la morphologie du système cardiovasculaire dépassaient en effet le cadre d’une réflexion éthérée et purement esthétique ou spéculative ²²⁹ dans la mesure où y étaient directement associés des enjeux de poids : il s’agissait de clarifier les fonctions du système cardiovasculaire et, plus précisément, d’obtenir des critères objectifs de désignation et de classification des anomalies de la ramification vasculaire pouvant conduire à des symptômes comme « l’anévrisme, les coussins intimaux, les plaques d’athérosclérose, l’effet Fahreus-Lingdvist et autres problèmes de flux sanguin » ²³⁰ . Murray adopte donc dès le départ une perspective de type « physiologie physique ». Il reprend en cela les travaux déjà anciens du médecin français Poiseuille (1799-1869) sur la circulation sanguine mais aussi ceux, plus récents et qualitatifs, de l’embryologiste allemand Wilhelm Roux (1850-1924) ²³¹ sur l’angle de ramification des artères. Murray part de l’hypothèse selon laquelle les sections et les angles des ramifications des vaisseaux sanguins, mais aussi des branches des arbres sont tels que la circulation qui s’y produit obéit au « principe du travail minimal » ²³² . Le travail qu’il faut selon lui minimiser est celui qui est nécessaire au maintien d’un flux (de sang ou de sève) à travers les vaisseaux ²³³ . En partant de cette hypothèse d’optimalité, qu’il qualifie de « Principe physiologique du travail minimum », Murray arrive à exprimer ce que l’on a appelé plus tard la « loi de Murray » pour les sections des vaisseaux et pour les angles de ramification.

Par rapport aux premiers travaux de Poiseuille sur la vitesse de la circulation sanguine et sur les forces qui lui font obstacle, l’hypothèse novatrice de Murray est donc double : d’une part, il faut selon lui attribuer au fonctionnement physiologique cette partie de la morphogenèse qui concerne la mise en place des ramifications vasculaires, d’autre part, il faut supposer qu’un principe d’optimalité préside à ce mécanisme comme on le suppose selon lui d’ordinaire dans les autres mécanismes physiologiques ²³⁴ .

La loi de Jean-Léon Poiseuille (1799-1869)

Le polytechnicien et médecin Jean-Léon Poiseuille a fait faire un pas important à la physiologie physique (de laquelle on peut distinguer la physiologie chimique, contemporaine et notamment promue par Liebig 235 ) lorsqu’il a mis au point en 1827 l’hémadynamomètre ou appareil à mesurer la vitesse du sang. Dans ce contexte de science expérimentale, Poiseuille a ensuite travaillé sur le frottement que la circulation des liquides ou des gaz rencontre dans des tubes de sections diverses (1844). Poiseuille se fondait sur l’hypothèse d’un écoulement laminaire, c’est-à-dire sur le cas dans lequel « les filets fluides restent parallèles à l’axe du tuyau » 236 . Et il ne considérait que les abaissements de pression interne en conformité avec la seule première composante du théorème de Bernouilli sur la circulation des fluides. Il négligeait enfin la pesanteur ainsi que les infiniment petits du second ordre dans l’expression différentielle des forces de viscosité 237 . Moyennant ces hypothèses assez lourdes, il est en effet possible d’exprimer le débit J d’un fluide de viscosité η circulant dans un tube de rayon a et longueur l en fonction de l’abaissement de pression ΔP :

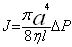
Cette loi de Poiseuille, proposée dans un contexte essentiellement expérimental, fait donc abstraction de certaines nécessités théoriques pourtant déjà reconnues. Ainsi, nous pouvons remarquer, après Pierre Costabel, que l’hydrodynamique est bien sans doute l’un des premiers domaines où « la mécanique classique et sa méthode d’analyse mathématique » ont été « tenues de composer avec les sciences physiques » 238 .

Or cette double hypothèse (explication de la morphogenèse par le fonctionnement physiologique, explication du fonctionnement physiologique par le principe d’optimalité) permet selon lui d’aboutir à une loi mathématiquement exprimable et quantifiable. Voici comment en substance.