Le principe du travail minimum en physiologie morphologique
Pour exprimer le travail déployé par le flux dans un vaisseau, Murray prenait donc en compte la force de freinage due à la viscosité du sang (conformément à la loi de Poiseuille 239 ) ainsi que l’énergie nécessaire au niveau métabolique pour maintenir le volume de sang dans les vaisseaux (énergie supposée dépendre essentiellement et directement de la surface totale de la paroi vasculaire). Il obtenait l’expression suivante :

où η est la viscosité du sang, m un coefficient métabolique, J le flux sanguin, a le rayon du vaisseau sanguin considéré et l la longueur de la portion du vaisseau 240 .
En minimisant W en fonction de a par dérivation, on obtient l’expression du flux en fonction du rayon :
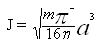
Or, comme les flux se conservent lors d’une ramification du vaisseau n°0 en deux vaisseaux n°1 et n°2, on peut écrire :
J0 = J1 + J2
La loi de Murray s’exprime alors ainsi pour les rayons des 3 vaisseaux :
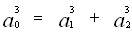
Il se trouve que cette loi est en effet très souvent observée dans les systèmes vasculaires. En travaillant sur de petits arbres botaniques et avec l’aide de deux assistantes, dès 1925, Murray montrait que cette relation était aussi approximativement valable pour les rayons des ramifications dans les plantes 241 . On note cependant que la valeur de l’exposant (ici 3) empiriquement mesurée peut varier quelque peu 242 .
Une autre « loi de Murray » semble également s’appliquer aux angles que font les vaisseaux les uns par rapport aux autres. Pour la mettre en évidence, Murray considérait cette fois-ci le système de la bifurcation dans son ensemble ainsi que le travail total qui s’y développe. Il prenait donc en compte la somme des travaux mécaniques Wi des sections 0, 1 et 2. On peut en effet y faire apparaître les angles de bifurcations par projection des flux sur les axes de coordonnées. En différentiant cette somme et en ayant recours au principe du travail virtuel élaboré par Lagrange, on obtient une expression du type 243 :
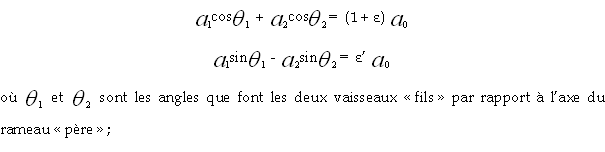
ε et ε’ (inférieurs à 0.1 en valeur absolue) représentent les déviations possibles par rapport à l’optimalité 244 .
Cette relation est également vérifiée empiriquement mais de façon beaucoup moins précise et stable que celle qui porte sur les sections ou rayons des vaisseaux. Tout au moins observe-t-on une conformité tendancielle ou qualitative : « quand un vaisseau de sang parent subit une bifurcation, la branche la plus large fait un angle plus petit avec la direction du parent que n’en fait la branche la plus étroite » 245 .