Le « modèle développemental » linéaire et les règles de réécriture

Comme il est non seulement un théoricien mais aussi un praticien de la biologie du développement, Lindenmayer ne propose pas de « modèle mathématique » nouveau sans se donner explicitement un terrain biologique qui pourrait convenir aux premiers essais de ce modèle. Le premier article de 1968 distingue donc le type d’objet biologique sur lequel un tel formalisme va être construit et essayé : les organismes filamenteux, c’est-à-dire ceux qui ont une structure multicellulaire filaire ou arborescente. L’intérêt de ces organismes est qu’ils facilitent l’introduction du formalisme des interactions cellulaires dans la mesure où ils permettent d’en réduire d’abord le nombre et la dimension. Ces objets réels simplifiés sont déjà en quelque sorte des objets théoriques. Un corps filamenteux possède des cellules dont le voisinage se réduit le plus souvent aux deux cellules latérales. L’introduction du formalisme pourra donc se faire très classiquement : d’abord simplement, en partant de ces organismes, puis par complexifications successives du voisinage cellulaire.

Pour produire un modèle mathématique formel de la croissance de tels organismes, Lindenmayer utilise donc la théorie mathématique des machines séquentielles ou théorie des « boîtes noires ». Cette théorie est inspirée, on l’a dit, de la machine de Turing, de la théorie des automates de von Neumann, mais aussi de la cybernétique. Trois ans plus tard, lorsqu’il évoquera cette période à l’occasion du 4ème Congrès International de Logique, de Méthodologie et de Philosophie des Sciences (organisé à Bucarest en 1971 ¹²³⁴ ), Lindenmayer avouera que c’est en fait essentiellement le livre d’introduction à la cybernétique de Ashby, paru en 1956 ¹²³⁵ , qui l’a aidé à concevoir ses premiers automates interactifs :

‘« J’aimerais ajouter ici que W. Ross Ashby (1956) a été parmi les premiers à énoncer clairement la méthode de construction valant pour les automates interactifs et je lui dois une dette pour l’apprentissage du principe de base de cette méthode. » ¹²³⁶ ’

C’est dans ce genre d’aveu que l’on comprend l’importance pour un biologiste de formation de disposer de bons ouvrages de vulgarisation ou d’introduction et qui soient faciles d’application dès lors qu’une nouvelle méthode formelle se fait jour. En 1968, Lindenmayer se sert donc des explications simplifiées de Ashby et définit pour sa part des cellules formelles qui possèdent une ou plusieurs entrées, des sorties et un état. La « machine séquentielle » représentant une seule cellule est donc pour lui un quintuplet rassemblant ¹²³⁷  :

• la fonction donnant l’état suivant de la cellule
• la fonction donnant la sortie suivante de la cellule
• les variables d’état
• les variables d’entrée
• les variables de sortie

Dans le système de Lindenmayer, les entrées des cellules correspondent aux sorties des cellules voisines : c’est bien en effet son but de rendre compte des relations intercellulaires dans la topologie des plantes. Mais ce qui est nouveau et décisif par rapport à la formalisation antérieure de Ulam ou de Apter, par exemple, c’est que Lindenmayer permet que l’état suivant d’une cellule soit un dédoublement c’est-à-dire une division,en terme biologique, de cette même cellule. Par là il veut formaliser une croissance pouvant se déclencher à n’importe quel endroit de l’organisme déjà formé. Ce n’est donc pas l’environnement qui fait naître spontanément les cellules, comme dans le modèle algorithmique d’Ulam, mais ce sont les cellules déjà vivantes qui « choisissent » ou non de se multiplier. Et ainsi l’organisme peut s’accroître. Pour exprimer ce modèle, Lindenmayer a abandonné la logique symbolique très sévère et purement syntaxique de Whitehead et Russell. Ainsi, pour représenter les fonctions de transitions a-t-il d’abord recours à des matrices récapitulatives ¹²³⁸ . Il est à noter que ce sont des représentations bidimensionnelles : elles se présentent sous la forme de tableaux à deux séries d’entrées. Lindenmayer rompt ainsi avec les représentations purement linéaires car préférentiellement linguistiques et anti-intuitivistes des Principia Mathematica et adopte une représentation mathématique de nature plus graphique ¹²³⁹ . Il confirme même cette évolution en adoptant conjointement une représentation de ces mêmes fonctions par ce qu’il appelle, à la suite des ingénieurs en automatique, des « diagrammes de transitions » ¹²⁴⁰ . Les états de la cellule y sont représentés par les sommets d’un graphe et les diverses arêtes orientées de ce graphe représentent les transitions possibles entre les états en fonction des entrées de la cellule. Enfin, il n’est pas possible d’utiliser le formalisme simple des automates à états et des fonctions de transition si l’on ne se donne pas également un procédé qui détermine la structure du temps, c’est-à-dire les instants où il faut appliquer de façon synchrone ces fonctions. C’est pourquoi un tel formalisme, comme le précise Lindenmayer, en plus de la discrétisation réaliste des parties de l’organisme, les cellules ¹²⁴¹ , nécessite la discrétisation du temps : comme dans la simulation de Cohen ou dans l’automate de Ulam, à chaque pas de temps, chaque cellule va appliquer ses deux fonctions de transitions.

Il faut alors que Lindenmayer arrive à modifier le formalisme habituel des fonctions de transition pour pouvoir représenter la croissance du filament par division d’une cellule mère en deux cellules filles. Il modifie de cette façon la matrice de transition des états des cellules ¹²⁴² :

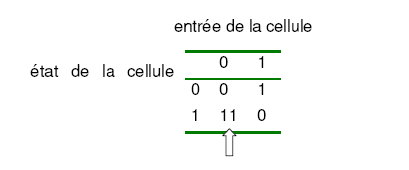
Le contenu des cases du tableau indique la valeur (0 ou 1) de l’état suivant de la cellule en fonction de son entrée actuelle et de son état actuel. Dans la case que nous avons indiquée par une flèche, on voit apparaître deux états. Ce qui indique en fait que l’on a affaire à deux cellules dont Lindenmayer spécifie les états, à leur naissance. Ici, chacune des cellules filles commencera donc avec un état à 1.

Ainsi, à la différence de la proposition de Eden, la croissance peut intervenir de l’intérieur de l’organisme en quelque sorte, comme un bourgeonnement, et non pas seulement sur ses bords comme une accrétion ou une agrégation, c’est-à-dire aux frontières de son corps avec l’environnement. Il y a là quelque chose qui correspond en effet davantage à la réalité biologique de la croissance d’un corps filamenteux. Avec ce formalisme, on perçoit une croissance ou un développement plus qu’une reproduction ou qu’une réplication. Cela est d’autant plus vrai que Lindenmayer n’en donne pas d’abord une représentation géométrique sur un plan quadrillé, comme le firent en revanche Eden, Ulam et Cohen. Il reste plutôt sensible aux relations à la fois hiérarchiques et historiques (ou généalogiques) de l’arbre symbolique qui se construit à partir de l’itération des règles de transition sur une séquence de 0 et de 1. Son premier modèle est en effet un tableau de 0 et de 1 à une seule colonne et où les cellules filles s’insèrent à la place de la cellule mère. Ce qui a pour effet de donner un modèle linéaire sous la forme d’une séquence binaire.