Le « rappel » et l’« application » de la théorie des files d’attente

C’est donc, comme nous l’avons vu, après avoir émis un doute sévère sur la fiabilité de l’enseignement immédiat des seules données quantifiées accessibles sur la présence des insectes dans les fleurs, que de Reffye procède à ce qu’il nomme un rappel de la théorie des files d’attentes. Pour ce faire, il s’en tient aux quelques hypothèses élémentaires (voir encadré) sans aucunement rappeler les démonstrations ni même justifier leurs hypothèses (comme celle de l’existence d’un régime permanent dans un processus aléatoire de type poissonien). Il a en effet dans l’esprit d’« appliquer » ¹⁶²⁸ ensuite directement ce « point de vue » à son problème sans assumer toutes les démonstrations qui ont servi à constituer cet outil formel. Il est cependant surprenant que ni lui-même ni les auteurs qui ont collaboré avec lui à ce travail ne songent à inscrire ces propositions de modélisation dans une filiation comme celle de la dynamique des populations qui fait explicitement usage des processus de Galton-Watson ¹⁶²⁹ (1874) depuis leur reprise par R. A. Fisher en 1922 et des processus de naissance et de mort depuis 1924 avec les premiers travaux de G. U. Yule ¹⁶³⁰ .

Rappel de la théorie des files d’attente Nous reprenons ici directement à l’article de 1980 son texte de présentation rapide. Voir [Reffye (de), Ph., Parvais, J.-P., Coulibaly, N. et Gervais, A., 1980], p. 86. Ce texte est lui-même très inspiré de la présentation habituelle qu’en fait Robert Faure. Les notations sont exactement les mêmes. Voir par exemple [Faure, R., Boss, J.-P. et Le Garff, A., 1961, 1967], pp. 54-59. , Nous avons repris ici les notations de [Reffye (de), Ph., Parvais, J.-P., Mossu, G. et Lucas, P., 1978], p. 255.

Il peut y avoir deux réponses à cette question. D’une part, les biologistes, les généticiens et les entomologistes qui entouraient alors de Reffye, au vu de leurs formations et de leurs centres d’intérêt antérieurs, n’étaient pas eux-mêmes très versés dans la modélisation mathématique issue de la dynamique des populations. L’entomologiste N. Coulibaly comme le biologiste cellulaire J.-P. Parvais ont plutôt suivi et accompli une formation de physiologistes. Ils regardent donc les phénomènes vivants d’interaction entre insectes et fleurs au mieux du point de vue de l’écophysiologie, mais pas du tout avec le regard de l’écologie ni de la dynamique des populations où primeraient pourtant les notions de prédateurs et de proie ainsi qu’elles furent introduites formellement dans les premiers modèles de Lotka et Volterrra. De Reffye lui-même avait été formé à l’amélioration des rendements et des plantes dans une perspective principalement physiologique ou de biologie cellulaire pour la sélection génétique. D’autre part, il faut reconnaître que l’objet étudié ici n’est pas formellement tout à fait identique à des processus de naissance, de mort ou de prédation tels qu’ils étaient encore majoritairement traités en France dans les années 1970 : c’est-à-dire avec le souci d’en venir le plus vite possible à une expression analytique (différentielle ou autre), au besoin difficilement soluble, des phénomènes considérés à un niveau agrégé. Les approches de l’écologie des populations elles-mêmes ne se focalisaient pas tant en effet sur la rencontre individuelle, sur le destin individuel du prédateur ou de sa proie, que sur la mise en place d’équilibres globaux au niveau de l’écosystème.

De son côté, la recherche opérationnelle, parce qu’elle s’est conçue davantage comme un art pluridisciplinaire, comme une science appliquée ou une science d’ingénieur, que comme une science pure, a en revanche développé moins d’énergie que l’écologie théorique ou même la biométrie à systématiquement rechercher des expressions analytiques pour ses modèles. Même si ses promoteurs affirment parfois l’importance des modèles analytiques ¹⁶³³ , la mise à disposition des calculateurs numériques dès les années 1950 dans ce secteur, et l’urgence de disposer de conseils effectivement opérationnels pour la décision économique et de gestion ont contribué à lui faire mettre au second plan cet objectif. De plus, de nombreux sectateurs de cette discipline ont œuvré à sa vulgarisation par la publication et la traduction d’ouvrages pédagogiques élémentaires et de référence, notamment, en France, aux éditions Dunod, dans la collection « Recherche opérationnelle » dirigée par Georges Darmois. Ce n’est donc pas un hasard que de Reffye ait davantage appris à maîtriser la manipulation des processus aléatoires avec cette discipline, pourtant davantage tournée vers l’économie et les sciences humaines en général, qu’avec la biométrie.

Dans la suite de l’article, de Reffye adapte le modèle général de processus poissonien au problème spécifique qui est le sien en faisant une hypothèse supplémentaire. En effet, on ne peut pas réellement considérer que les insectes fassent la queue dans une fleur. Mais ils se répartissent dans la fleur sans trop se gêner a priori. Ce qui peut mathématiquement s’exprimer de la façon suivante dès lors que l’on dispose du modèle poissonien : « Le taux de service est proportionnel au nombre N de clients dans la station. » ¹⁶³⁴

Dès lors, la probabilité de trouver N insectes dans la fleur à un instant donné est exprimable explicitement en fonction du nombre l d’insectes arrivants et du nombre m d’insectes disposant du service à ce moment-là :

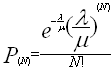
En secouant les fleurs, ce qui a pour effet de la vider de ses occupants, en répertoriant et en dénombrant ensuite les nouveaux insectes arrivés sur elle au bout d’une minute, il est possible d’évaluer pour chaque espèce d’insecte le taux d’arrivée l intervenant dans la loi d’arrivée horaire et qui s’exprime en nombres d’insectes par fleur et par heure. En répertoriant tous les insectes observés à un moment donné sur un grand nombre de fleurs (8020 fleurs à Bingerville, par exemple), il est également possible d’évaluer la distribution des files d’attentes, c’est-à-dire le nombre de fois où l’on a trouvé une fleur avec 0, avec 1, avec 2, …, avec N insectes. On peut alors calculer empiriquement la loi d’arrivée P(N). Comme on dispose par ailleurs de sa formulation explicite (la formule précédente) en fonction des m_N, on peut donc reconstituer le débit m_N des insectes passant au « service », avec N insectes par heure, ainsi que le temps t_N moyen de stationnement de chacun des N insectes (t_N = 1/m_N).