2.1. Jeu de données et méthodes d’analyse

Pour mener à bien cette expérimentation, nous avons utilisé une matrice contenant les profils de chaque bâti habité du terrain d’étude, soit plus de 38 000 objets géographiques. Chaque objet est caractérisé par la valeur brute de ses indices de synthèse construits pour chacun des thèmes étudiés. Deux exceptions sont à noter. Le thème de la sécurité a été exclu de l’analyse multicritère en raison de la faible qualité des données sources alors que le thème de l’habitat a été évincé de l’analyse du fait du format qualitatif de l’indice de synthèse (la taille des logements a en effet été obtenue par analyse typologique). Huit critères servent donc de référence à cette analyse multicritère :

• le transport en commun : l’indice de synthèse exprimé en capacité moyenne/jour caractérise la disponibilité et la proximité de l’ensemble des modes de transports en commun (métro, funiculaires, tramway et bus) ;
• l’accidentologie : l’indice de dangerosité des infrastructures routières prend en compte la densité et la gravité des accidents de la route ;
• les commerces et services de proximité : l’indice de synthèse exprime à la fois la densité et la diversité des commerces et services ;
• le bruit : l’indice présente l’exposition théorique (exprimée en dB) à la nuisance sonore due à la circulation automobile. Ces valeurs sont issues d’une modélisation de la propagation du bruit de la circulation en milieu urbain.
• la pollution atmosphérique : l’indice représente la concentration en dioxyde d’azote (µg/m3) liée à la circulation automobile. Ces valeurs sont issues d’une modélisation de la dispersion de la pollution d’origine routière en tissu urbain ;
• la propreté des rues : l’indice exprime la fréquence moyenne (en nombre de passages par semaine) de nettoiement au voisinage des bâtiments. Cette moyenne est calculée par pondération des longueurs de tronçons de chaque unité de voisinage ;
• la disponibilité des espaces verts : l’indice de synthèse exprime à la fois l’attractivité et la diversité des usages des espaces verts disponibles ;
• les équipements scolaires : l’indice de synthèse prend en compte la présence des différents établissements et la continuité de l’enseignement scolaire.

L’analyse multicritère nécessite d’importantes ressources matérielles informatiques. L’ampleur de notre jeu de données (plus de 38 000 enregistrements caractérisés par 8 critères) interdisait, dans l’état de nos moyens, tout traitement exhaustif direct de l’ensemble du jeu de données. Nous avons donc opté pour un traitement à deux niveaux, méthode dite de la classification par paliers successifs, ce qui nous permet de fractionner le jeu de données tout en conservant l’intégralité de sa diversité. Dans un premier temps, toutes les fractions du jeu de données initiales ont été classifiées, puis une deuxième classification a été appliquée à l’ensemble des types issus de la première phase.

Plusieurs approches étaient alors possibles pour le fractionnement initial du jeu de données : soit selon un découpage géographique, soit par tirage aléatoire. Un premier test de fractionnement a été effectué sur une base géographique à raison d’un échantillon par arrondissement. Ce choix permet d’obtenir des échantillons dont la taille est compatible avec les moyens informatiques mis à notre disposition. Cette alternative permet également d’obtenir des résultats cartographiques interprétables et transposables à la connaissance préalable du terrain d’étude. Cette méthode comporte néanmoins un biais. Certains phénomènes étudiés ayant une incidence spatiale marquée, il est possible que l’expression géographique de l’un des critères caractérise entièrement l’un des échantillons. Dans ce cas, ce critère s’impose comme une constante non déterminante pour tous les types issus de l’analyse de cet échantillon, alors même qu’il est discriminant à l’échelle de l’ensemble du jeu de données. Ce fait s’est produit pour le sixième arrondissement pour lequel les résultats ont été altérés par l’influence prédominante du parc de la Tête d’Or au travers du critère « espaces verts ».

Nous nous sommes donc orientés vers une méthode de fractionnement aléatoire : le jeu de données a été divisé aléatoirement en deux échantillons qui ont été classifiés chacun séparément. Le type de classification retenu est la classification ascendante hiérarchique (C.A.H.) selon la méthode de Ward. Le principe de la classification hiérarchique consiste à construire une « suite de partitions en n classes, n-1 classes, n-2 classes…, emboîtées les unes dans les autres, de la manière suivante : la partition en k classes est obtenue en regroupant deux des classes de la partition en k+1 classes. Il y a donc au total n-2 partitions à déterminer puisque la partition en n classes est celle où chaque individu est isolé et la partition en une classe n’est autre que la réunion de tous les individus. On parle de classification hiérarchique ou de hiérarchie, car chaque classe d’une partition est incluse dans une classe de la partition suivante » ¹⁸⁴ . La suite des partitions obtenues est usuellement représentée sous la forme d’un arbre de classification (dendrogramme). La hiérarchie dans le dendrogramme est « indicée »582 car à chaque partition correspond une valeur numérique représentant le niveau auquel ont lieu les regroupements ; plus l’indice est élevé plus les parties regroupées sont hétérogènes. Cet indice est aussi appelé « niveau d’agrégation 582». Connaissant l’arbre de classification, il est facile d’en déduire des partitions en un nombre plus ou moins grand de classes, il suffit pour cela de couper l’arbre à un certain niveau et de regarder les « branches » correspondantes. « Le principal problème des méthodes de classification hiérarchique consiste à définir le critère de regroupement de deux classes, ce qui revient à définir une distance entre classes. Tous les algorithmes de classification hiérarchique se déroulent de la même manière : on recherche à chaque étape les deux classes les plus proches, on les fusionne, et on continue jusqu’à ce qu’il n’y ait plus qu’une seule classe 582 ».

La méthode de Ward que nous avons utilisée repose sur le principe suivant : les deux classes pour lesquelles la perte d’inertie interclasse (ou variance interclasse : moyenne des carrés des distances des centres de gravité de chaque classe au centre de gravité total) est la plus faible sont fusionnées. Ceci revient à réunir les deux classes les plus proches en prenant comme distance entre elles la perte d’inertie que l’on encourt en les regroupant. En effet, une bonne partition est celle pour laquelle l’inertie interclasse est forte (inertie intraclasse faible), c’est-à-dire celle qui regroupe les individus les plus proches et sépare les plus éloignés. Cela démontre que lorsque l’on passe d’une partition en k+1 classes à une partition en k classes en regroupant deux classes en une seule, l’inertie interclasse ne peut que diminuer. La classification ascendante hiérarchique procède ainsi par regroupements successifs des unités élémentaires en fonction de leurs ressemblances par rapport à un ensemble de critères. Cette méthode a été choisie à la fois parce qu’elle permet de traiter des échantillons de grande taille avec des ressources informatiques raisonnables et parce qu’elle a généralement tendance à aboutir à une répartition relativement homogène des types. Le choix du niveau de classification, et donc du nombre de classes retenu, s’est fait sur la base de l’examen du dendrogramme : au total, 18 classes ont été retenues pour chacun des deux échantillons.

La démarche consiste ensuite à effectuer la synthèse par classification des types issus de l’étape précédente. Chacun des types issus de cette première étape est ainsi défini par la valeur moyenne de chacun de ses critères. Nous obtenons par conséquent une matrice de 36 lignes pour 8 colonnes. Cette classification a pour but de regrouper les types issus de la phase précédente en types similaires. Pour cette phase, nous avons de nouveau opté pour une classification ascendante hiérarchique selon la méthode de Ward.

Figure V.3. Dendrogramme pour la C.A.H. de synthèse pour l’échantillon par arrondissement

Figure V.4. Dendrogramme pour la C.A.H. de synthèse pour l’échantillon aléatoire

Au regard des deux figures, il apparaît clairement que nous aboutissons sensiblement au même résultat par un tirage aléatoire ou par un échantillonnage par arrondissement. Les deux dendrogrammes incitent à retenir une classification en 3, en 5 ou en 6 classes avec une stabilité remarquable pour chacune de ces trois possibilités. Nous pouvons dès lors représenter ces classes dans l’espace géographique et procéder à une analyse de leurs profils dans cet espace.

En analyse de données, il est d’usage de procéder d’abord à une analyse descriptive. L’analyse en composantes principales (A.C.P.) peut être considérée comme la méthode de base dans un cas comme le nôtre où nous travaillons sur un tableau individus/caractères numériques. Elle consiste à réduire le nombre de caractères initiaux afin de pouvoir représenter géométriquement les individus et les caractères par leurs projections sur des plans dits principaux. La réduction des caractères initiaux se fait par la construction de nouveaux caractères synthétiques obtenus en combinant les caractères initiaux au moyen des « facteurs ». Elle n’est possible que si les caractères initiaux ne sont pas indépendants et ont des coefficients de corrélation non nuls.

Lorsque la taille de l’échantillon n’est pas trop grande, il est donc généralement d’usage de réaliser d’abord une A.C.P. pour étudier le « comportement » des observations et des variables par leurs projections sur les plans principaux, puis éventuellement une C.A.H. dans le but de construire des classes homogènes. Dans le cas où l’on obtient un axe principal expliquant une part importante de l’inertie (variance), il est envisageable de faire une C.A.H. sur les coordonnées des projections des individus sur cet axe. L’A.C.P. et la C.A.H. sont considérées comme des méthodes complémentaires l’une de l’autre. Dans notre cas, remarquons d’abord que les variables n’ont pas de coefficients de corrélations très marqués.

Figure V.5. Matrice des corrélations

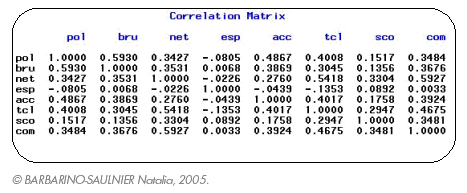
Cette matrice de corrélation témoigne d’une assez bonne corrélation entre les variables « bruit » et « pollution », « commerces » et « nettoiement », ou encore entre « transports en commun » et « nettoiement ». La variable « espaces verts » quant à elle semble totalement indépendante des autres. Par ailleurs, la taille de l’échantillon (38 083 observations) explique, d’une part, cette faible dépendance entre les variables, et d’autre part, ne nous permet pas d’avoir une représentation intéressante des individus sur les axes principaux (nous obtenons un nuage de point non interprétable sur un plan). Notre objectif étant d’aboutir à une typologie, nous avons donc d’abord procédé à une C.A.H. dont les résultats sont directement interprétables par les profils des classes dans l’espace géographique. Nous avons ensuite fait une A.C.P. en incluant les profils des classes obtenues en tant qu’individus supplémentaires, afin de pouvoir les projeter sur les plans principaux retenus. Un programme d’A.C.P. dans le logiciel SAS nous donne les valeurs propres, facteurs et composantes principales suivantes.

Figure V.6. Histogramme de valeurs propres

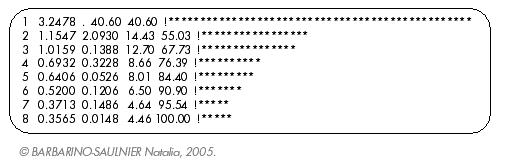
La somme des valeurs propres correspondant à l’inertie totale est égale à 8 car nous avons centré-réduit les données initiales. Les trois premières valeurs propres expliquent 67,73% de l’inertie, et nous résumerons donc les données par les trois premières composantes principales. En effet, compte tenu de la taille de l’échantillon et de la faible dépendance des variables, nous pouvons considérer que cette réduction des caractères initiaux est suffisamment significative.

Figure V.7. Interprétation des composantes principales et des axes 1 et 2

Figure V.8. Interprétation des composantes principales et des axes 1 et 3

Figure V.9. Interprétation des composantes principales et des axes 2 et 3

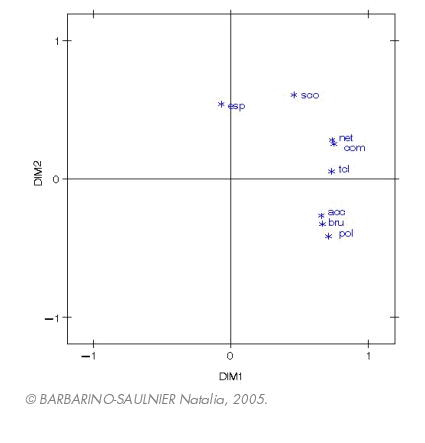
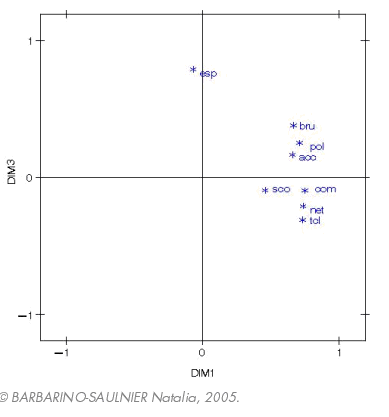
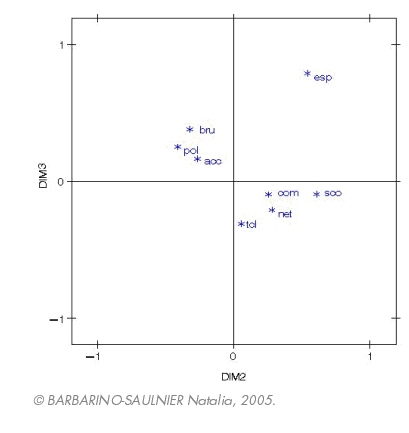
L’examen de ces trois figures permet d’interpréter les composantes principales et de repérer rapidement les groupes de caractères liés entre eux ou opposés, à condition toutefois que les points soient proches de la circonférence (cercle de corrélation non tracé ici). Nous remarquons tout d’abord que la première composante qui explique pourtant 40% de l’inertie, n’apporte pas d’information particulière en ce sens où elle n’oppose pas clairement de caractères entre eux. Nous voyons ensuite que dans les trois plans, la variable « espaces verts » reste isolée des autres et semble ainsi jouer un rôle à part entière. C’est également le cas de la variable « scolaires » mais dans une moindre mesure. Pour les autres variables, le plan constitué par les composantes 2 et 3 ne donne pas une qualité suffisante de représentation car les variables sont trop éloignées du cercle de corrélations.

Lorsque nous regardons les projections sur les deux autres plans principaux, nous remarquons que deux groupes de caractères s’opposent assez clairement (sur les composantes 2 et 3) : un groupe constitué des variables « bruit », « pollution » et « accidentologie » et un autre constitué par « commerces », « nettoiement » et « transports en commun ». Dans les plans formés, l’un par les composantes 1 et 3, l’autre par les composantes 2 et 3, nous pouvons remarquer que la variable « scolaire » est assez proche du « paquet » « commerces, nettoiement, transports en commun ». Nous pouvons interpréter cela de la manière suivante : si cette variable paraît relativement indépendante au regard du premier plan principal, les deux suivants semblent indiquer qu’elle est, malgré tout, relativement dépendante de « commerces, nettoiement, transports en commun ».

D’un point de vue géographique, nous pouvons tirer les conclusions suivantes :

• là où l’on trouve du bruit, se concentrent également la pollution et les accidents (le long des axes de circulation structurants) ;
• le réseau de transports en commun semble cohérent avec la distribution des commerces et services alors que la qualité du nettoiement semble être assez bien corrélée avec ces deux critères ;
• l’implantation des établissements scolaires semble être relativement corrélée avec le jeu de caractères « commerces », « nettoiement » et « transports en commun », mais dans une moindre mesure.
• l’accessibilité aux espaces verts, quant à elle, semble totalement indépendante de tous les autres critères.

Les éléments évoqués le sont de manière relativement intuitive, ce qui est rassurant quant à la qualité du jeu de données initial. Ces conclusions nous permettent d’accéder à une sorte de « logique d’organisation » du territoire décrite par les différents critères de qualité de vie. Très schématiquement, nous pouvons présupposer que le groupe « commerces, nettoiement, transports en commun, scolaires» signe un territoire urbain dense et central s’opposant à une marge plus faiblement équipée où l’automobile, rendue nécessaire, apporte son lot de nuisances. Néanmoins, les faibles corrélations entre variables ainsi que le comportement indépendant des « espaces verts » laissent supposer de nombreuses situations particulières. Le dépouillement de la C.A.H. doit faire apparaître à la fois des types répondant à un schéma global et des types qui s’en extraient. Ces conclusions restent donc à vérifier par la représentation cartographique des résultats.