1.1.3. Pertinence, cohérence et mesurabilité des modèles de demande directe

Les modèles de demande directe présentent un certain nombre d'avantages. Ces modèles sont calés sur des séries chronologiques, ce qui est a priori un gage de fiabilité par rapport à des modèles calés sur de la variance en coupe instantanée. Toutefois, ces modèles ne sont pas exempts de critiques.

• En termes de pertinence

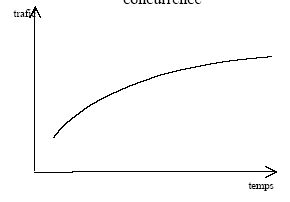
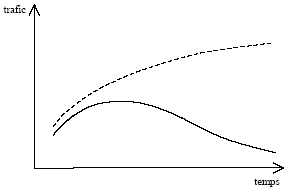
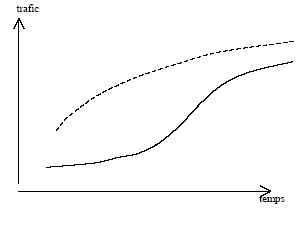
La forme des modèles de demande directe est bien adaptée pour modéliser l'évolution d'un marché global. En revanche, dans le cas d'un système de transport où règne une forte concurrence entre les modes, il existe une logique de génération – partage modal : la demande de transport croît corrélativement à la croissance économique et à l'amélioration de la qualité du réseau, avant de se répartir entre les différents modes suivant leurs niveaux de performance. Or la précédente démarche ne permet pas d'appréhender ce phénomène. Compte tenu du phénomène sous-jacent génération – partage modal, il est probable que les élasticités ne sont pas constantes, du moins pas dans le cas de modes fortement soumis à la concurrence d'autres modes. Dans le cas du train, qui est progressivement concurrencé par l'avion, il peut même y avoir inversion du signe de l'élasticité au PIB (Figure 3). Initialement, le train est peu concurrencé par l'avion : plus le PIB augmente, plus le trafic total et donc le trafic train augmente ; au fur et à mesure que le PIB augmente, la valeur du temps des voyageurs augmente, les individus basculent sur l'avion ; il peut arriver un stade où le transfert de clients du train vers l'avion l'emporte sur la croissance globale du marché ; l'élasticité au PIB devient négative. Pour l'avion, mode qui "l'emporte" sur le train, l'élasticité a le mérite de rester toujours du même signe, même s'il existe un risque de rupture de pente (Figure 4). Utiliser un modèle de demande directe pour modéliser des modes fortement soumis à la concurrence est ainsi dangereux. Toutefois tout dépend du contexte. Si un mode est largement majoritaire par rapport aux autres, les élasticités relatives à ce mode seront peu sensibles à la concurrence (Figure 2). Une équation de demande directe peut être éventuellement approximativement adaptée.

Dans le cas de la modélisation d'un marché global tous modes confondus, il se peut que les élasticités ne soient pas tout-à-fait constantes non plus. En effet, le marché global peut être la superposition de plusieurs marchés aux élasticités différentes (marché des motifs professionnels et marché des motifs personnels, marchés de la moyenne et de la très longue distance) : au fur et à mesure que la part des marchés à fortes élasticités augmente, l'élasticité du marché total augmente. Inversement, il peut se produire des phénomènes de saturation : pour un marché donné, l'élasticité peut décroître. Il peut aussi se produire des effets doubles offre de transport / PIB : au fur et à mesure que l'offre s'améliore, l'élasticité au PIB est susceptible d'augmenter. Prendre en compte ce type de phénomène dans la formulation n'est pas toujours aisé, compte tenu du nombre limité de points d'observation. Ceci étant, et contrairement au cas d'une tentative de modélisation d'un mode soumis à une forte concurrence, les élasticités ont le mérite de ne pas changer de signe.

Une autre limite des modèles de demande directe calés sur séries temporelles réside dans le nombre nécessairement très limité des facteurs explicatifs. Le nombre de points à disposition pour le calage est en effet généralement assez limité : une vingtaine d'années, ce qui limite considérablement le nombre de variables qu'il est possible de prendre en compte. Lorsque les données à disposition sont des données trimestrielles, il est possible de modéliser des dynamiques temporelles de façon plus fine. Il est possible d’introduire plus de variables dans la modélisation. En contrepartie, la complexité du modèle croît en raison des phénomènes de saisonnalité. Dans le cas de données annuelles, il est délicat de prendre en compte des phénomènes de retards, sauf éventuellement la prise en compte d'un unique retard, soit sur la variable à expliquer, soit sur une des variables explicatives. Quant aux facteurs explicatifs, ils se limitent forcément à quatre ou cinq, ce qui est peu.

Par ailleurs, les variables explicatives des modèles de demande directe sont nécessairement très agrégées. Or, une même variation d'un indicateur de vitesse moyenne ou de produit moyen peut correspondre à des états différents de variation de la structure tarifaire ou de la structure des vitesses, donc à des impacts différents sur les trafics. Il est souhaitable de prendre en compte dans la modélisation à la fois le niveau moyen de l'indicateur et la structure de cet indicateur. L'introduction de cet indicateur de structure est néanmoins problématique. D'une part se pose la question de la méthode de modélisation de l'indicateur et de son opérationnalité. D'autre part il ne faut pas trop multiplier les coefficients supplémentaires à calibrer pour une question de nombre de degrés de libertés suffisants. Un cas intéressant est celui où une variable varie de façon homogène sur l'ensemble des liaisons et des segments de marché (cas de la chute du prix de la route par opposition aux variations de vitesse ferroviaire). Dans ce cas le problème de structure ne se pose plus.

Les modèles de demande directe semblent ainsi assez bien adaptés pour modéliser des modes de transport :

• suffisamment "autonomes" (suffisamment majoritaires ou suffisamment peu sensibles à la concurrence des autres modes pour que les élasticités de la formulation de demande directe puissent être considérées comme constantes),
• dont l'essentiel des variations dépendent de quelques facteurs peu nombreux et pour lesquels les variations des variables explicatives sont homogènes avec un impact homogène sur les différents segments du marché.

Dans les autres cas leur mise en œuvre est plus délicate.

• En termes de cohérence

Les modèles de demande directe ne sont pas nécessairement totalement cohérents. Ainsi dans le cas où on modélise les trafics ferroviaires et aériens par des modèles de demande directe, les élasticités des trafics ferroviaires et aériens par rapport au prix du fer sont estimées dans le cadre de processus séparés et vont en sens contraires (négatif dans le cas du fer, positif dans le cas de l'air). Rien ne garantit qu'au final l'élasticité de la demande totale air + fer par rapport au prix du fer soit négative et qu'elle reste négative en projection. Nous pouvons définir une plage sur laquelle ces élasticités restent de signe correct, restreignant ainsi la plage de validité du modèle. Toutefois les élasticités peuvent être biaisées tout en étant de signe correct.

• En termes de mesurabilité

Un avantage des modèles de demande directe est de toujours disposer de données opérateurs globales en séries chronologiques, même si l'homogénéité des séries dans le temps n'est pas toujours garantie. Par ailleurs utiliser de la variance temporelle pour caler des élasticités temporelles est a priori un gage de fiabilité par rapport à l'utilisation de variance spatiale pour en déduire des élasticités temporelles.

Toutefois le calage des modèles de demande directe n'est pas sans inconvénient : le nombre de points d'observations est souvent limité, ce qui réduit drastiquement le nombre de variables possibles. Les variables sont presque toujours fortement corrélées ce qui réduit la variance temporelle exploitable donc la fiabilité du calage. La multicolinéarité et le risque de régressions fallacieuses constituent les principaux ennemis des séries temporelles.

• La multicolinéarité

Les variables explicatives des séries temporelles sont généralement fortement corrélées, ce qui est susceptible d'entraîner des problèmes dans l'estimation. En théorie, la multicolinéarité ne constitue pourtant pas un problème rédhibitoire. Si une multicolinéarité au sens strict (cas où il existe une relation parfaitement linéaire entre les variables explicatives, ce qui ne se réalise jamais totalement en pratique), rend impossible l'estimation des paramètres, une multicolinéarité au sens large (il existe une - éventuellement forte - corrélation entre au moins deux variables explicatives) permet mathématiquement l'estimation des paramètres du modèle. Dans le cas d'une multicolinéarité au sens large (qui est le problème qui nous préoccupe) l'estimation des coefficients des variables reste possible. La multicolinéarité constitue pourtant un phénomène "gênant" (Rys, Vaneecloo, 1998). "En effet, dans ce cas, les estimations des coefficients des variables sont covariantes, de sorte que la précision de chacune d'elles devient incertaine (et d'autant plus incertaine que les corrélations entre variables explicatives sont importantes). Cela peut même les rendre non significatives" (Rys, Vaneecloo, 1998). Dans le cas d'une multicolinéarité importante (supérieure à 0,9), l'estimation des coefficients des variables corrélées accorde beaucoup de poids aux (nécessairement petites) différences de variations entre les variables corrélées, ce qui tend à gonfler le poids des erreurs de mesure des variables explicatives ; ceci peut entraîner des écarts significatifs sur les paramètres dans le cas de petits échantillons. Le risque est de voir une variable récupérer l'effet des variables qui lui sont corrélées. Tant que les variables restent corrélées dans la phase de projection, ce n'est pas un problème. Dans le cas contraire, les simulations sont biaisées.

Or il n'existe pas de véritable thérapeutique au problème de multicolinéarité (Rys, Vaneecloo, 1998). La seule vraie solution serait d'augmenter le nombre de données "l'augmentation du nombre de données [réduisant] l'effet de la colinéarité statistique, même si celle-là reste au même niveau" (Rys, Vaneecloo, 1998). Malheureusement, les séries chronologiques de trafic à disposition portent généralement sur 20 à 30 années, pas plus. Une solution à la multicolinéarité souvent recommandée consiste à réécrire le modèle en variations. En effet, "les variations des variables sont en général beaucoup moins colinéaires que les variables elles-mêmes" (Rys, Vaneecloo, 1998). De plus, en économie, toutes les variables sont entraînées par les mêmes mouvements économiques généraux, les variables présentes dans l'équation captent l'influence de la variable absente, ce qui peut gonfler de manière trompeuse le R² et entraîner un biais dans les estimations. Travailler en variations permet de contourner cet écueil. Le modèle en variations est en général beaucoup plus sévère que le modèle initial : le R² chute généralement de façon spectaculaire. Toutefois, comme le soulignent (Rys, Vaneecloo, 1998) :

‘"Le travail en variations ne peut pas être considéré comme un remède à la colinéarité. [En effet], "les hypothèses faites sur le résidu théorique du modèle en variations sont incompatibles avec celles faites sur le modèle initial. Si on appelle e_t le résidu du modèle initial et u_t celui du modèle en variations, on peut écrire pour tout t u_t = e_t+1 - e_t ou encore e_t+1 = e_t + u_t. Supposer la nullité des espérances mathématiques des résidus e et u n'amène aucune contradiction ; en revanche on ne peut supposer l'absence d'autocorrélation et la constance de la variance de l'un des résidus sans enfreindre l'une de ces hypothèses pour l'autre résidu. En effet de deux choses l'une :
– ou nous supposons que les u_t sont indépendants entre eux et de variance constante V(u) ; dans ce cas, le résidu e est marqué par une hétéroscédasticité (u_t et e_t étant indépendants V(e_t+1)=V(e_t)+V(u_t) ; la variance du résidu e croît avec le temps), et par une autocorrélation positive : (COV(e_t+1,e_t)=E(e_t+1e_t)=E[(e_t+u_t)e_t]=E(e_t²)+E(u_te_t)=V(e_t)>0
– ou nous supposons que les e_t sont indépendants entre eux et de variance constante V(e) ; dans ce cas, il n'y a pas hétéroscédasticité pour u (car V(u_t)=V(e_t+1)+V(e_t)=2V(e)), mais il y a autocorrélation négative (car COV(u_t+1,u_t)=E[(e_t+2-e_t+1)(e_t+1-e_t)]=-V(e_t+1)<0).
Le travail en variations n'est donc pas une thérapeutique de la colinéarité dans le modèle initial. Les deux formulations correspondent à deux représentations théoriques différentes des mécanismes qui régissent l'évolution de la grandeur Y au cours du temps : dans le modèle initial, si cette grandeur s'est située au-dessus de sa valeur normale (c'est-à-dire si e _t est positif), il n'y a pas de raison pour que cette tendance se maintienne à la période suivante. Au contraire, dans le modèle en variations, si la croissance a été plus forte que la normale (c'est-à-dire si u _t est positif), le terrain ainsi gagné par Y n'est pas perdu, puisque la variation qu'elle connaîtra s'effectuera à partir du niveau déjà atteint. Dans le premier cas, le résidu aléatoire ne fait que produire des écarts de part et d'autre de la trajectoire réglée par l'évolution des variables explicatives : quels que soient les aléas, les trajectoires réelles s'enrouleront autour de cette trajectoire de base et se ressembleront toutes plus ou moins. Dans le second, les résidus s'inscrivent dans la trajectoire, de sorte que le cumul des aléas peut conduire à des trajectoires très diversifiées." (Rys, Vaneecloo, 1998). ’

Il existe plusieurs types d'approches dans les séries temporelles : les modélisations sur variables en niveaux, les modélisations sur variations de variables, et les modélisations sur taux de croissance des variables (Durand, 2001 ; Gabella-Latreille, 1997). Même si modélisations sur variables en niveau et modélisations sur variations ou taux de variations de variables semblent être équivalents au vu de leur écriture mathématique, il s'agit bien de deux représentations théoriques différentes dont les estimations conduisent à des modèles différents. Dans le cas des modèles en variations et en taux de variations, il n'existe généralement pas de multicolinéarité entre les variables. En revanche, dans les modèles sur variables en niveau, le niveau de corrélation est généralement important et il n'existe pas véritablement de solution idéale à ce problème, si ce n'est de poser comme condition pour appliquer le modèle en projection le maintien des corrélations.

• Le risque de régression fallacieuse

L'autre difficulté dans les régressions linéaires sur séries temporelles réside dans le risque de régressions fallacieuses, compte tenu de l'existence quasiment systématique d'un trend sous-jacent. Le risque est d'obtenir des élasticités biaisées malgré un excellent R² et des t de Student très élevés (Salanié, 1999). Pour s'assurer que tel n'est pas le cas, il est nécessaire de regarder la statistique de Durbin – Watson ²⁹ . Un DW anormal peut être le signe d'une autocorrélation des résidus mais il peut aussi être le signe d'autres anomalies : erreur de spécification, omission d'une variable importante, changement à un moment donné du régime qui détermine la variable expliquée. En fait un DW anormal est plus souvent le signe d'une de ces trois maladies que le signe d'une autocorrélation du résidu théorique (Rys, Vaneecloo, 1998).