2.3.1.3. L’indicateur de Theil
L’indice de Theil (1967) mesure l’écart entre le poids d’un individu (ou d’un groupe) dans la population et le poids de son revenu dans le revenu total 1 . Sa valeur varie entre 0, la situation d’égalité et log N, dans le cas où tous les revenus sont nuls, sauf un.
Soit y i le revenu de l’individu i appartenant à une population de N individus et µ le revenu moyen, l’indice s’écrit :
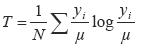
Cet indice accorde un peu plus d’importance à l’inégalité dans le bas de la distribution qu’à l’inégalité parmi les riches. Moins couramment utilisé que l’indice de Gini, l’indice de Theil présente néanmoins des atouts pratiques incontestables. Son principal intérêt est de pouvoir se décomposer à l’infini en partitionnant la population puis en redécomposant chacun des groupes en différents sous-groupes, cela afin d’analyser l’évolution des inégalités dans et entre différentes sous-populations. Cependant son expression mathématique, qui utilise la forme logarithmique, limite son usage à des valeurs non nulles.