I.2. Le modèle en taux de croissance

Le modèle double-logarithmique est un modèle couramment utilisé en dépit de biais liés à l’utilisation de séries temporelles et de l’hypothèse d’élasticité constante qu’il suppose. Si le modèle en taux de croissance est beaucoup moins utilisé que le modèle double-logarithmique, il permet néanmoins d’estimer la relation entre la demande de transports de marchandises et le PIB en introduisant l’hypothèse d’une élasticité variable.

Ce modèle est au cœur de la thèse de Céline Gabella-Latreille réalisée au laboratoire d’économie des transports, un travail également appelé le modèle quin-quin fret (Gabella-Latreille, 1997). Ce modèle postule qu’il existe une relation linéaire entre le taux de croissance de la demande de transport de marchandises et le taux de croissance de la production industrielle, soit :

Cette équation montre que l’élasticité de la demande de transport de marchandises par rapport à la production industrielle est inversement proportionnelle au taux de croissance de l’indice de production industrielle. En d’autres termes, cela signifie que l’élasticité de la demande de transport de marchandises par rapport à la production industrielle est variable. D’un point de vue économétrique, l’hypothèse d’une relation à élasticité variable est acceptée si la constante α de la relation (1.6) est significativement différente de zéro.

La Figure 2 illustre le modèle en taux de croissance en représentant la relation entre les taux de croissance de moyen terme ⁴ des tonnages terrestres intra-nationaux en France ⁵ et celui de la valeur ajoutée de l’ensemble de la branche industrielle entre 1980 et 1994. Cette figure illustre la forte significativité de ce modèle.

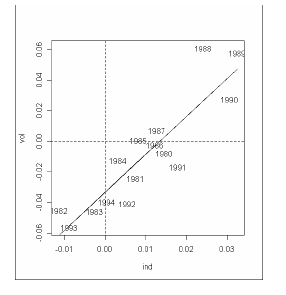
Le modèle estimé présente en effet un coefficient de corrélation ajusté de 78% et la valeur des coefficients estimés est significativement différente de zéro. L’équation estimée est la suivante :

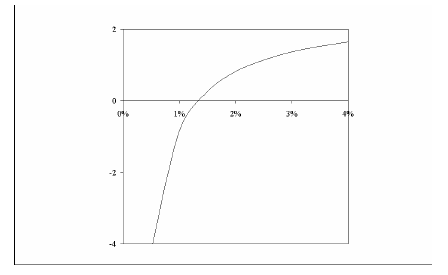
La valeur de la constante estimée est significativement négative. Ceci signifie que l’hypothèse d’une élasticité constante peut être rejetée. D’autre part, en suivant l’équation (1.7), il ressort de cette estimation que l’élasticité estimée croît avec le taux de croissance de la VA de l’industrie (Figure 3). Les volumes de transports de marchandises amplifient alors la croissance industrielle. Ce phénomène est à mettre sur le compte des phénomènes de stockage et de déstockage de la production industrielle.

Ce modèle a été utilisé à diverses reprises au laboratoire d’économie des transports. Le travail de Gaballa-Latreille (1997) estime ainsi un modèle en taux de croissance de moyen terme en désagrégeant le transport national de marchandises par catégorie de produits (i. e. par chapitres NST). Cette relation est estimée pour le transport terrestre de marchandises en France entre 1971 et 1991. Céline Gaballa-Latreille observe que l’élasticité de la demande de transport de marchandises par rapport à l’indice de production industrielle est variable et, la constante de la relation affine estimée étant significativement négative, croissante en fonction du taux de croissance de l’indice de production industrielle. Des recherches réalisées au laboratoire d’économie des transports ont prolongé ce travail en appliquant ce modèle à la demande de transport de marchandise entre la France et l’Italie ⁶ (LET, 1997a) ou à la demande de transport de marchandises dans la vallée du Rhône (Gabella-Latreille, 1999).

Il est au final étonnant d’observer le nombre limité d’applications du modèle en taux de croissance car de nombreux économistes des transports estiment que rien ne justifie a priori l’hypothèse d’une élasticité constante. Un groupe d’experts en économie des transports explique ainsi :

‘ La table-ronde s’est plu […] à mettre en garde les chercheurs contre la tentation d’utiliser des modèles à élasticité constante pour caractériser les relations entre la croissance économique et la croissance des transports. Le monde de transports est en effet un univers à élasticité variable : les relations entre la mobilité et le PIB ne sont pas constantes, mais au contraire variables et, en outre, elles peuvent être sujettes à inflexion politique (CEMT, 2002, p.197).’

Ce constat souligne la pertinence du modèle en taux de croissance par rapport au modèle double-logarithmique. La tentation d’utiliser des modèles à élasticité constante peut alors s’expliquer par le peu d’intérêt traditionnellement porté par les chercheurs à ce champ d’investigation. La plupart des recherches appliquées en matière de prévision de la demande de transport de marchandise est effet réalisée en dehors du champ académique. Il est dès lors peu surprenant de voir ces recherches s’orienter vers des modèles simples et, en apparence, significatifs comme le modèle double-logarithmique en dépit de sérieux biais tenant tant à la pertinence du modèle (e. g. hypothèse d’élasticité constante) qu’à ses propriétés économétriques (e. g. non stationnarité des variables, auto-corrélation des erreurs).

L’économétrie standard permet donc d’estimer la relation entre le transport de marchandises et l’activité économique ou industrielle grâce au modèle en taux de croissance ou au modèle double logarithmique. En pratique, l’estimation du second modèle est privilégiée pour estimer les déterminants de la génération de la demande de transport malgré des limites importantes. De ce point de vue, le développement de l’économétrie des séries temporelles a renouvelé l’analyse des séries temporelles (Bresson et Pirotte, 1995). La sous-section qui suit revient sur les développements permis par l’application de ces techniques économétriques à la relation entre la demande de transport de marchandises et l’activité industrielle ou économique.