Partie 2. Estimation économétrique du couplage transport/économie : le cas du transport transalpin
La partie qui précède a montré que la relation entre la demande de transport de marchandises et l’activité économique était au cœur des modèles de prévision de la demande. Cette partie s’est toutefois contentée d’une analyse générale de cette relation. L’objet de la présente partie poursuit cette recherche en étudiant cette relation sur un territoire précis : celui des traversées alpines. L’orientation de cette partie est donc clairement empirique. Aussi convient-il en premier lieu d’observer que cette recherche n’est pas inédite puisque de nombreux modèles de prévision ont déjà estimé la relation entre la demande de transport à travers les Alpes et la production économique. En suivant un rapport d’expertise du LET (1997a), une présentation d’Alain Rathéry (2000) ou un rapport de la CEMT (CEMT, 2001), une revue des principaux modèles alpins de prévision souligne la prépondérance des travaux réalisés hors du champ académique.
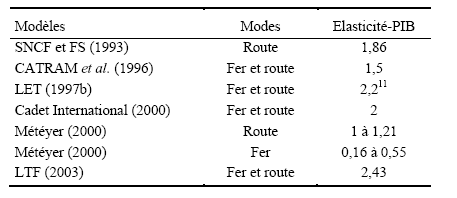
Par exemple, une étude des FS et de la SNCF (FS et SNCF, 1993) estime les volumes des différents marchés du transport ferroviaire (i. e. transport ferroviaire combiné, fer conventionnel et autoroute ferroviaire) à horizon 2010. Dans cette recherche, présentée en détail dans un rapport d’expertise du LET (1997a), trois modèles indépendants sont réalisés pour prévoir la demande de chaque sous-marché ferroviaire. Un modèle de prévision de la demande globale de transport routier est estimé à partir d’un modèle économétrique double-logarithmique pour prévoir la demande potentielle de l’autoroute ferroviaire. Pour le transport entre la France et l’Italie, l’élasticité (constante) de la demande de transport par rapport au PIB est estimée à 1,86. Elle est supposée décroître au-delà de l’année 2002.
Un groupe de bureaux d’études conduit par CATRAM (CATRAM et al.,1996) a également réalisé un modèle alpin de prévision. L’objectif de ce modèle, commandé par le GIP Transalpes 9 , est d’estimer la demande globale de transport de marchandises à travers les Alpes à horizon 2010. Contrairement au modèle FS/SNCF, l’exercice CATRAM estime la demande globale de transport terrestre de marchandises avant de répartir la demande globale entre les différents modes. Il s’agit donc d’une modélisation par étapes où un premier sous-modèle de génération est suivi d’un second sous-modèle de répartition. Le sous-modèle de génération de l’exercice CATRAM propose une analyse économétrique de la relation entre la demande de transport de marchandises et le PIB à partir d’un modèle double-logarithmique. Une élasticité-PIB (constante) de 1,5 est retenue pour la demande de transport terrestre dans le Nord des Alpes françaises.
Le laboratoire d’économie des transports (LET, 1997b) a également réalisé pour le compte du GIP Transalpes un modèle de prévision de la demande de transport de marchandises à horizon 2015. Ce modèle, dit modèle quin-quin fret France-Italie (QFFI), s’inscrit dans la tradition des modèles quin-quin fret réalisés au LET (Gabella-Latreille, 1997 ; Durand, 2001). Le modèle distingue une étape de génération de la demande et une étape de répartition modale. L’étape de génération de la demande est construite autour de l’estimation d’un modèle à élasticité variable. La valeur de ces élasticités est élevée. L’élasticité de la demande de transport par rapport à l’indice de production industrielle italien est de 2,2 pour le scénario médian (croissance de l’indice de production industrielle de 2% par an).
Le bureau d’études Cadet International (2000) a également réalisé un modèle de prévision de la demande de transport de marchandises pour le compte du GIP Transalpes. Ce modèle a pour objectif de prévoir la demande de transport de l’autoroute ferroviaire en 2015. La méthodologie retenue dans ce modèle est celle d’une modélisation en deux étapes. La première étape du modèle est un modèle de génération de la demande de transport de marchandises. Une élasticité de la demande de transport routier par rapport au PIB italien égale à deux est estimée. Cette élasticité est supposée décroître après 2005.
Au sein du ministère des transports, le SES a développé un modèle de prévision de la demande de transport transalpin. Météyer (2000) présente les hypothèses de ce modèle de demande de transport. Les élasticités retenues sont des élasticités variables. Pour le scénario médian (1,9% de croissance économique), l’élasticité est légèrement supérieure à l’unité pour le transport routier de marchandises et proche de 0,5 pour le transport ferroviaire.
Enfin, un modèle de Lyon-Turin Ferroviaire 10 (2003) prévoit la demande de transport de la nouvelle ligne ferroviaire entre Lyon et Turin à horizon 2030. Il s’agit d’un modèle en deux étapes. La première étape du modèle est un modèle de génération de la demande de transport à l’échelle de l’arc alpin étendu de Vintimille au Tauern. Des élasticités doubles-logarithmiques sont estimées à partir de séries temporelles. Une élasticité de la demande globale de transport de marchandises par rapport au PIB Italien de 2,43 est utilisée. L’élasticité est supposée décroître au-delà de 2010.
Ces modèles estiment donc un ensemble d’élasticités de la demande de transport par rapport à la production économique (Tableau 8). Les élasticités estimées sont significativement supérieures à l’unité à l’exception du transport ferroviaire selon Météyer (2000). Elle sont significativement plus élevées que les élasticités estimées dans la littérature (cf Tableau 1, p.38).
A ces travaux, il convient d’ajouter la recherche Environmental Sustainable Transport (EST) conduite pour l’OCDE (1997). Cette recherche prospective dont la partie française a été réalisée par le bureau d’études ENERDATA propose une approche originale dite de backcasting (par opposition à forecasting). L’objectif de cette approche n’est pas d’estimer si la demande de transport augmente sous l’effet de la croissance de la production économique mais de savoir comment la demande de transport de marchandises peut se diriger vers des volumes de transport pré-déterminés :
‘Il ne s’agit plus dès lors de projeter comment la croissance économique détermine la demande de transport, mais d’analyser comment l’évolution de la demande de transport peut tendre vers un niveau et une structure pré-déterminés, de façon compatible avec la croissance économique et démographique. La notion même d’élasticité de la demande de transport au PIB est alors remise en cause, sauf à considérer l’élasticité comme un ratio a posteriori entre deux taux de croissance largement « découplés » (Château et Morcheoine, 2001, p.121).’Cette approche est originale, voire hétérodoxe. Elle se distingue des modèles standards de prévision car elle ne cherche pas à prévoir la trajectoire la plus probable mais s’oriente vers des trajectoires volontairement alternatives. En ce sens, elle permet d’éclairer la méthodologie prospective.
Au final, deux conclusions ressortent de cette brève revue des modèles alpins. La première conclusion est que la littérature s’est largement développée en dehors du champ académique. La seconde conclusion découle de la première : les estimations étant largement réalisées en dehors du champ académique, elles se caractérisent par l’utilisation de techniques économétriques frustes et biaisées. La plupart des modèles ont en effet recours à une spécification double-logarithmique en dépit des limites de ce modèle. Ce constat pourrait rappeler celui de Granger et Newbold (1974), trente ans plus tôt :
‘We find it very curious that whereas virtually every textbook on econometric methodology contains explicit warnings of the dangers of autocorrelated errors, this phenomenon crops up so frequently in well respected works 11 (Granger et Newbold, 1974, p.111).’Considérant d’une part le caractère fruste des estimations proposées pour estimer la relation entre la demande de transport de marchandises à travers les Alpes et l’activité industrielle et, d’autre part, la rareté des travaux réalisés dans le champ académique sur le sujet, il semble donc qu’il existe encore un espace pour une analyse économétrique des facteurs déterminant la demande de transport de marchandises à long terme. La présente partie propose d’estimer les facteurs déterminant la demande de transport de marchandises à travers les Alpes en utilisant des spécifications économétriques qui ne soient pas des régressions fallacieuses (spurious regressions) pour reprendre l’expression de Granger et Newbold.
Deux spécifications économétriques sont successivement estimées. Dans un premier temps (chapitre trois), un modèle à élasticité variable est estimé. Cette estimation s’inscrit dans la lignée des différentes versions du modèle quin-quin fret réalisées au laboratoire d’économie des transports. Prenant acte du renouvellement de la littérature permis par l’application des modèles issus de la co-intégration, un modèle à correction d’erreur est estimé dans le chapitre quatre.