II.1. Test de co-intégration

Tableau 48. Test ADF pour le modèle [1], résidus de l’équation de long terme

Figure 18

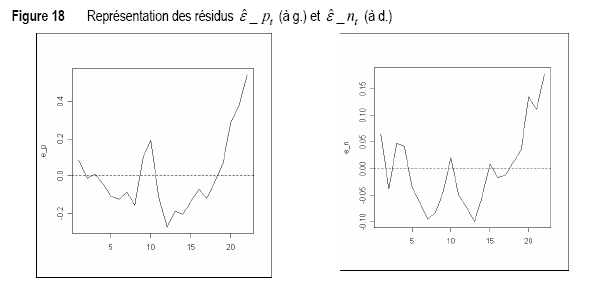
Brown, Durbin et Evans (1975) proposent un test de stabilité temporelle des relations basé sur le calcul des résidus récursifs (Bresson et Pirotte, 1995, pp.312-315).

En considérant l’erreur de prédiction à une étape

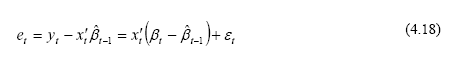
il est possible de définir les résidus récursifs des prévisions comme les erreurs de prédiction normalisées ou :

Le test CUSUM ¹⁵ au carré est alors basé sur le calcul de la quantité :

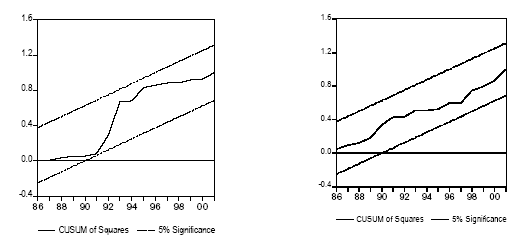
Le test du CUSUM carré est usuellement représenté sous une forme graphique. La valeur de la statistique doit alors évoluer, sous l’hypothèse nulle de stabilité de la relation, entre deux droites représentant les bornes de l’intervalle. Ce test CUSUM est donc réalisé pour tester l’hypothèse de stabilité des relations de long terme estimées entre les séries p _t et n _t et la série i _t .

La Figure 19 montre alors que l’hypothèse de stabilité de la relation de long terme ne peut être acceptée au seuil de 5%. Cette figure souligne l’instabilité de la relation au cours des dernières années de l’observation.

Figure 19. Le test CUSUM-carré pour la relation entre la série i t et les séries p t (à g.) et n t (à d.)

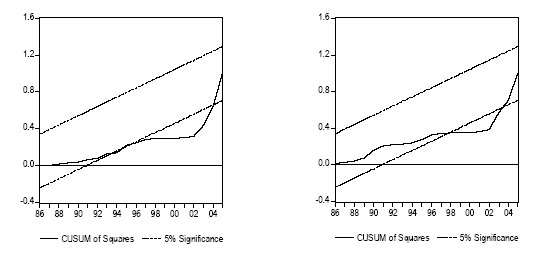
L’instabilité de la relation de long terme au cours des dernières années de l’estimation est aisée à expliquer à partir des conclusions du Chapitre 3. Dans ce chapitre, il a en effet été montré que la demande de transport de marchandises continuait à augmenter au cours de cette période en dépit du recul de l’activité industrielle italienne. Il est alors logique d’observer que la relation de long terme estimée est instable au cours de la période d’étude puisque le modèle de long terme estimé est un modèle à élasticité constante.

Il est en revanche possible d’observer que, pour la demande d’échange bilatéral franco-italien, la relation de long terme estimée ne présente pas de caractéristiques d’instabilité selon le test CUSUM-carré (Figure 20). Dans le chapitre qui précède, il a également été montré que, contrairement aux deux autres types de demande de transport transalpin, la demande d’échange bilatéral franco-italien n’augmentait pas durant la période [2002-2005] de recul de l’activité industrielle italienne. Cette différence entre la demande de transport d’échange franco-italien et les demandes de transport de transit littoral et nord-européen explique pourquoi la demande de transport d’échange franco-italien et l’activité industrielle italienne sont des séries co-intégrées contrairement aux autres types de demande de transport transalpin.

Figure 20. Le test CUSUM-carré pour la série f

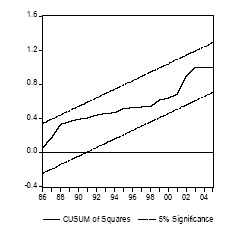
Dans ce qui suit, il est proposé de re-considérer la relation de long terme entre les demandes de transport de transit nord-européen et littoral et l’activité industrielle italienne en retirant la période d’instabilité mise en évidence (autrement dit, en retirant les quatre dernières observations).

En se restreignant à la période [1984-2001], la relation de long terme entre la demande de transport de type p ou n et l’activité industrielle italienne devient stable au sens du test CUSUM carré (Figure 21).

Figure 21. Le test CUSUM-carré pour les séries p (à g.) et n (à d.) restreintes à la période [1984-2001]

Tableau 49. Test ADF pour le modèle sans constante ni tendance pour les résidus de l’équation de long terme restreinte

Au terme de cette sous-partie, plusieurs conclusions peuvent être formulées. Il apparaît en premier lieu que la relation entre la demande de transport de marchandises d’échange bilatéral franco-italien et l’activité industrielle italienne est une relation de co-intégration. Ensuite, il apparaît qu’il n’existe pas de relation de co-intégration entre la demande de transport de marchandises de transit littoral ou la demande de transport de transit nord-européen et l’activité industrielle italienne. Ce phénomène s’explique par l’instabilité de la relation de long terme au cours des périodes de recul de l’activité industrielle italienne. Durant ces périodes, la demande de transport de marchandises ne diminue pas malgré un repli de l’activité industrielle. Il y a alors une divergence entre les sentiers de croissance de la demande de transport de marchandises et celui de la production industrielle. Enfin, en retirant la période [2002-2005] d’instabilité de l’échantillon, la relation de long terme devient stable au sens du test CUSUM-carré. Il apparaît également qu’en retirant cette période de l’échantillon, les séries p_t ou n_t et la série i_t sont également des séries co-intégrées.

Cette partie montre qu’il existe une relation de co-intégration entre la demande de transport de marchandises à travers les Alpes et l’activité industrielle italienne. Il est donc pertinent d’utiliser un modèle à correction d’erreur pour estimer la relation entre ces variables comme ceci est fait dans la sous partie qui suit en suivant la procédure en deux étapes d’Engle et Granger (1987).