Lexique, Générateur et évaluateur
Dans TO les représentations sous-jacentes et de surface existent mais elles sont nommées respectivement l’input (entrée) et l’output (sortie). La manière dont TO détermine l’output à partir de l’input est totalement différente des théories générativistes traditionnellement dérivationnelles. Les théories dérivationnelles, comme leur nom l’indique, sont basées sur un traitement sériel de l’input, alors que dans TO, l’input y subit un traitement en parallèle. En effet, malgré le fait que les contraintes en TO soient hiérarchisées dans un ordre particulier, elles permettent de déterminer quel output est optimal en l’évaluant en parallèle. Une forme de surface, ou output, est considérée comme optimal quand elle satisfait le mieux à l’ordre relatif des contraintes. La grammaire de TO est donc un simple mécanisme qui apparie un output avec un input pour que chaque input ait précisément un, et un seul output (voir (28)). D’où le terme de théorie de la correspondance associé à la version la plus utilisée de cette théorie.
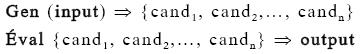
Pour accomplir cette fonction, la grammaire contient trois composants : le Lexique (Lex), le Générateur (Gen) et l’Évaluateur (Éval). Le premier composant, qui est le Lexique, est essentiel. Il conserve toutes les formes lexicales qui seront des inputs pour le Générateur (racines, affixes…). Il n’existe aucune contrainte agissant au niveau du Lexique. Le second, le Générateur, crée, à partir d’un input, une infinité d’outputs possibles qui sont nommés « candidats ». Chacun de ces candidats constitue une analyse logiquement possible de l’input donné. Enfin, le dernier composant, qui est l’Évaluateur, est chargé, comme son nom l’indique, d’évaluer les candidats à la sortie grâce à un ensemble de contraintes hiérarchisées. Il sélectionnera alors le candidat optimal parmi tous les candidats possibles. La fonction de ces trois composantes est résumée en (29).

Le générateur a comme propriété essentielle d’être libre de générer n’importe quel candidat à la sortie qui soit concevable (propriété nommée « liberté d’analyse »). 10 La seule restriction imposée à tous les candidats à la sortie est qu’ils soient formés à partir d’éléments possibles du vocabulaire universel des représentations linguistiques (structure segmentale, structure prosodique comme la syllabe ou le pied, morphologie comme les affixes ou les racines, syntaxe…). Une fois que Gen a généré tous les candidats possibles à l’output pour un input donné, la grammaire de TO n’a pas besoin de règles pour les transformer en réel output (transformation en série), comme déjà mentionné, tous les changements structuraux sont évalués en parallèle dans l’Éval. L’Éval est le composant central de la grammaire. Bien que Gen génère les candidats à l’output, c’est Éval qui va évaluer leur adéquation grâce à son système hiérarchisé de contraintes. Éval va ainsi estimer le nombre de violations de contraintes que chaque candidat sous-tend, pour chaque contrainte présente dans la grammaire, et ainsi sélectionner le candidat le plus adéquat, c’est-à-dire le candidat optimal. Ce candidat optimal représente l’output produit par le locuteur.
La hiérarchie des contraintes présente dans Éval contient toutes les contraintes universelles (cet ensemble de contraintes est appelé Con). Ces contraintes, comme nous l’avons déjà souligné, sont hiérarchisées différemment selon la langue. Le français et l’anglais auront ainsi le même ensemble de contraintes mais ces contraintes n’auront pas la même hiérarchie dans chacune de ces langues. Chaque contrainte de cet ensemble doit être classée au sein de la hiérarchie. Ceci signifie qu’il n’existe pas, en théorie, de contrainte ayant un rang indéterminé. Afin de rendre compte de la variation, certains auteurs ont proposé qu’une grammaire puisse contenir une hiérarchie partielle des contraintes, ce qui signifie que l’ordonnancement entre certaines contraintes soit indéterminé dans la hiérarchie (p. ex. Anttila 1997, Anttila et Cho 1998). Si on fait abstraction des contraintes dont la hiérarchie est indéterminée, pour les autres, les relations de dominances sont transitives (30).
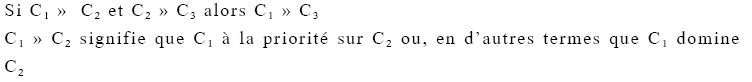
En ce qui concerne les marques de violations, chaque candidat se voit marquer autant de fois qu’il enfreint une contrainte. Ce nombre de marques peut, potentiellement, varier de zéro à l’infini. Toutefois, dans le but de déterminer un candidat optimal, un nombre infini de violation de contraintes n’est, dans la pratique, jamais pertinent. En effet, d’après Prince et Smolensky (1993 : 27), l’évaluateur considère uniquement l’absence d’une marque de violation ou sa présence ou le plus ou moins grand nombre de marque de violation pour une contrainte. Ce système ne détermine jamais le nombre de violation (il ne les compte pas) mais établit des comparaisons. En effet, chaque violation de contrainte sert un but : éviter la violation d’une contrainte plus élevée dans la hiérarchie. Ainsi, Prince et Smolensky (1993) postule l’existence d’un principe général d’économie (31).

Ceci implique qu’Éval n’évalue pas une infinité de candidats mais seulement ceux qui ont le plus de chance d’être optimaux suivant ainsi la loi de l’économie.
Enfin, Éval, pour sélectionner le candidat optimal, utilise un procédé par lequel chaque ensemble de candidats est réduit jusqu’à ce qu’un seul candidat soit disponible. Au départ, l’ensemble des candidats fourni par Gen, se trouve confronté à la première contrainte (la plus élevée dans la hiérarchie). De cette confrontation ne ressortiront que les candidats qui ne violent pas cette contrainte. Les candidats survivants passeront alors à la deuxième contrainte qui éliminera elle aussi les candidats qui la transgressent, réduisant leur nombre, et ainsi de suite. Ainsi, à chaque passage devant une contrainte, le nombre de candidats est réduit au vu de la violation de cette contrainte par certains candidats. Le processus, qui évalue en parallèle, pour chaque contrainte, tous les candidats survivants, se termine une fois qu’il ne reste plus qu’un candidat en course. Celui-ci deviendra le candidat optimal, l’output, même s’il viole des contraintes moins élevées dans la hiérarchie. Ceci est dû au principe de stricte domination explicité en (32).

Ainsi l’optimalité ne nécessite aucun compromis entre les contraintes de rangs différents. Pour illustrer ces principes, le fonctionnement de la grammaire de TO et les conventions représentationnelles couramment utilisées dans la littérature utilisant cette théorie, je vais maintenant présenter quelques exemples. Prenons deux contraintes A et B, deux candidats (a) et (b) et deux langues X et Y. Voici un tableau de résolution des conflits pour chacune des deux langues en présence, en (33) pour la langue X et en (34) pour la langue Y. Pour ces deux langues hypothétiques, l’ordre des deux contraintes est inversé.


Dans ces tableaux, l’input est donné dans la case en haut à gauche. Les candidats à l’output sont en dessous, notés ici (a) et (b). Il faut remarquer que les outputs potentiels sont toujours numérotés par des lettres afin de faciliter leur référence. Les contraintes apparaissent à droite de l’input dans l’ordre exigé par leur hiérarchie dans la langue en question (contrainte dominante à gauche, contrainte dominée à droite). Toute transgression de contrainte est marquée d’un astérisque dans la case appropriée. Le candidat optimal (c’est à dire le candidat qui est phonétiquement réalisé, donc le candidat grammatical) est celui qui obéit à la contrainte dominante; c’est le candidat (a) dans le tableau (33) et le candidat (b) dans le tableau (34). De façon redondante, mais pour faciliter l’interprétation visuelle des tableaux, le candidat optimal est généralement identifié à l’aide d’un index pointé vers la droite. De plus, les marques qui causent l’élimination d’un candidat sont suivies d’un point d’exclamation. Toujours pour faciliter la lecture des tableaux, les cases situées à droite de ces violations fatales, qui sont sans conséquence sur la décision finale, sont ombragées.
On peut constater à partir des exemples ci-dessus que les deux langues possèdent les mêmes contraintes mais ne réalisent pas phonétiquement le même output du fait de la hiérarchisation différente des contraintes appliquée à chacune de ces langues. Dans la langue X, c’est la contrainte A qui domine la contrainte B, alors que c’est l’inverse dans la langue Y. Par conséquent, l’output de chaque langue sera différent : ce sera le candidat (a) qui sera l’output de la langue X car il ne transgresse pas la contrainte la plus élevée alors que c’est l’inverse dans la langue Y.
Dès qu’un candidat réussit moins bien qu’un autre candidat sur une contrainte dominante, il est automatiquement éliminé, même s’il satisfait les contraintes dominées et que l’autre candidat les transgresse toutes. C’est l’application du principe de stricte domination. Un exemple en est donné dans le tableau (35).

Dans ce tableau, le candidat (a) est le candidat optimal, bien qu’il ne satisfasse qu’une seule des trois contraintes (la contrainte A) alors que le candidat (b) en satisfait deux (les contraintes B et C). La raison en est que la contrainte A domine les trois autres contraintes, c’est donc elle qui est déterminante dans la décision. Un autre cas de stricte domination est présenté en (36).

Le candidat (a), dans ce tableau, est toujours le candidat optimal, bien qu’il transgresse deux fois la contrainte B alors que le candidat (b) ne la transgresse pas. Ici encore la domination est stricte : quel que soit le candidat qui enfreint la contrainte la plus élevée (et si au moins un autre candidat ne la transgresse pas), il est exclu même s’il respecte toutes les autres contraintes moins élevées dans la hiérarchie.
Il n’existe donc pas d’élément de compromis dans la notion d’optimalité. L’évaluation des candidats par l’ensemble des contraintes est basée sur ce rapport de stricte dominance. Il n’existe donc pas de satisfaction de contraintes moins élevées qui puisse compenser la violation d’une contrainte plus élevée. Malheureusement, toutes les interactions de contraintes ne sont pas toujours aussi simples. Ce n’est pas toujours un candidat optimal qui satisfait la contrainte la plus élevée, enfreinte par tous les autres candidats, qui sera l’output. En effet, le candidat optimal peut présenter un certain degré de violation. La violation d’une contrainte est, par elle même, une condition insuffisante pour postuler l’agrammaticalité d’un candidat.
Le but de l’éval est de trouver un unique candidat qui sera le plus harmonique. Si une contrainte élimine tous les candidats en une seule fois, il ne restera aucun candidat qui pourrait être optimal. Pour éviter ce genre de désagrément, il faut concevoir qu’une certaine violation doit être causée par les candidats pour continuer l’évaluation. Il existe deux cas de figures où ce problème peut se poser. Le premier est le cas d’une violation multiple d’une contrainte par un même candidat qui de ce fait est éliminé (37). Le deuxième est le cas où une contrainte moins élevée permet de faire la différence entre deux candidats comme dans le tableau (38).


Dans le tableau (37), les deux candidats enfreignent la contrainte la plus élevée dans la hiérarchie. On constate, par contre, que même s’il même s’il n’enfreint pas la contrainte B (comme le fait le candidat (a)), le candidat (b) enfreint deux fois la contrainte A (la plus élevée), il est alors exclu de l’évaluation. C’est donc, dans cet exemple, le candidat (a) qui est le plus harmonique et donc optimal. Dans cette situation intervient la sévérité de la violation. Une forme qui présente le moins de violations de la contrainte la plus élevée (ici, la contrainte A) est préférée à une forme qui possède des marques de violations plus nombreuses pour la même contrainte.
Dans le tableau (38), on constate que la contrainte A est enfreinte le même nombre de fois par les deux candidats. Pour résoudre ce problème et pouvoir obtenir un candidat optimal, les deux candidats, pour être plus finement évalués, passent à la contrainte suivante qui sera décisive. Ainsi le candidat (a) qui viole la contrainte A mais pas la contrainte B sera déclaré optimal, puisque le candidat (b) transgresse à la fois les contraintes A et B. Par conséquent, les contraintes les moins élevées ne sont pas forcément rendues inactives par des contraintes plus élevées, mais leur violation n’est évitée que dans certaines conditions. Elles peuvent être enfreintes par un candidat optimal, mais leur violation doit être minimale, c’est-à-dire non fatales. Les contraintes dominées peuvent donc être toutes actives comme le montre le tableau (39).

On retrouve dans le tableau (39), tous les problèmes rencontrés jusqu’à présent, ce qui montre que les interactions entre contraintes sont parfois complexes. On peut constater, dans cet exemple, que toutes les contraintes sont actives pour déterminer quel sera le candidat optimal. Le candidat (d) est éliminé dès la première contrainte (la plus élevée dans la hiérarchie) car il transgresse celle-ci même s’il n’en enfreint aucune autre (stricte domination). Le candidat (c), qui satisfait la première contrainte, est éliminé par la deuxième car il comporte deux marques de violations de cette contrainte par rapport à ses concurrents, les candidats (a) et (b), qui n’en comportent qu’une chacun. Ces deux derniers candidats, qui ne violent pas la contrainte A et ne possèdent qu’une marque de violation pour la contrainte B, sont départagés par la contrainte C. Le candidat (a) qui ne transgresse pas la contrainte C, contrairement au candidat (b), est considéré comme le candidat le plus harmonique ; il est le candidat optimal.
Durant cette première partie, nous avons vu comment se structurait la grammaire de TO autour de trois composants Lex, Gen, et Éval, et comment Éval sélectionnait un output optimal grâce à son ensemble de contraintes hiérarchisées. Or, rien n’a été dit sur la nature des contraintes contenues dans Éval. Je vais donc, dans la prochaine section, présenter les deux familles de contraintes que l’on trouve en TO et décrire les plus importantes d’entre elles qui seront utilisées dans le chapitre 4.