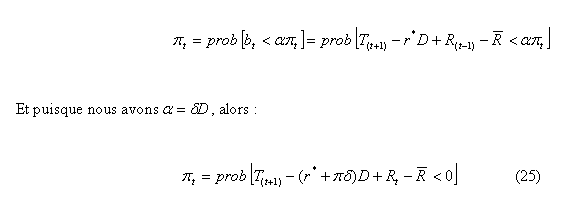3.1.1. Modèle avec clause de sortie pour une seule économie contaminée
A l’instar du modèle de Jeanne (1997), Masson a développé un modèle simple avec clause de sortie. Pour ce faire, il se base, sur un modèle de balance de paiement avec deux pays A et B. Il a exprimé les bénéfices totaux b t , pour le maintien de la parité, en fonction d’un ensemble de variables fondamentales clés :

Il est clair pour Masson, comme c’est le cas pour Jeanne (1997), que ces fondamentaux n’agissent pas d’une manière déterministe (comme dans Krugman, 1979). En effet, l’origine de la baisse des réserves repose essentiellement sur l’évaluation subjective des investisseurs internationaux de la solvabilité du pays. Cependant, la taille des dettes extérieures D, considérée par Masson comme exogène pour des raisons de simplification, est une variable cruciale dans la possibilité de la multiplicité des équilibres. En effet, une augmentation du taux d’intérêt, destinée à défendre la monnaie nationale implique simultanément un alourdissement de la charge de la dette externe, pouvant engendrer une chute des réserves de change et déclencher la crise d’une manière auto-réalisatrice.
Nous développons cette idée de Masson, dans ce qui suit, de façon plus formelle. Pour qu’un investisseur étranger, neutre vis à vis du risque, se place sur le marché domestique, il faut que la relation de la parité du taux d’intérêt (PTI) soit vérifiée :
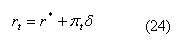
avec, r t : le taux d’intérêt domestique 32 .
C’est à dire que cet investisseur demande à être rémunéré par un montant égal au taux international supposé sans risque, plus une compensation égale à la probabilité de dévaluation π multipliée par la taille de dévaluation δ. Ce montent reflète le risque de dévaluation. Cependant, dans Jeanne (1997), nous avons vu que la probabilité de dévaluation dépend aussi des fondamentaux futurs notamment le taux d’intérêt sur les dettes extérieures, anticipés par ces investisseurs internationaux. En fait, c’est cette dépendance qui donne lieux à des équilibres multiples.
En utilisant l’équation (10), Masson propose une équation centrale formellement identique à ce que nous avons vu chez Jeanne (1997). Nous rappelons que cette équation centrale exprime la probabilité d’une dévaluation, dans une seule économie :