Ainsi, nous déduisons que le problème de l’endogénéité est caractérisé par les équations simultanées qui sont résumées dans la supposition que la matrice A n’est pas diagonale. Cependant, le problème de l’omission des variables est modélisé par la présence des chocs communs non observables z _t . Enfin, il est clair que le problème de l’hétéroscédasticité figure dans les deux matrices de variance covariance des chocs structurels  _t ou du choc commun z _t .

En s’inspirant de la définition de Forbes et Rigobon pour la contagion, le test de la contagion se base sur le test de la stabilité des paramètres (A et/ou  ) de notre système multivarié. Toutefois, nous constatons l’impossibilité de l’estimation du système (14). En effet, le nombre de paramètres est beaucoup plus grand que les nombres d’observations. Nous ne pouvons pas estimer alors les coefficients avec information complète.

Sachant les restrictions standards sur le système (14 b) à savoir :

• 1/ la normalisation à l’unité de la diagonale de A,
• 2/ la non corrélation des chocs structurels ( _t ),
• 3/ la stabilité des paramètres  et ,

il y aura donc 4 variables inconnues (, , V(  _1t ) et V(  _2t )). Avec les 3 équations du système (14b), le modèle (14a) demeure non identifié. Par conséquent, pour résoudre ce problème d’identification, nous devons ajouter d’autres restrictions additionnelles afin de rendre soluble le système donné par (14b) et identifier par la suite le système des équations simultanées (14a). Pour ce faire, Rigobon (2000) a utilisé une autre restriction ajoutée aux restrictions 1/ et 3/ :

• 4/ l’hétéroscédasticité engendrée par le changement entre les deux régimes (s = 2), est détectée seulement à travers une variance relative à un seul choc parmi les chocs structurels.

Ainsi, nous aurons 5 variables inconnues : , , la variance du choc pour chaque régime et la variance du choc qui engendre l’hétéroscédasticité, pour le premier régime. En effet, la prise en compte du changement de cette variance non conditionnelle, permet de contrôler le biais de l’hétéroscédasticité. Toutefois, nous disposons de 6 équations de covariances. Donc, puisque le nombre des équations de covariances est plus grand que le nombre de variables, le système est alors sur-identifié. Nous pouvons désormais contrôler aussi le biais de l’endogénéité ⁷² . Dans ce cas, il est possible de tester la stabilité des paramètres  et .

Cependant, le biais de l’omission des variables est contrôlé par l’introduction de la variable z _t dans le modèle (14). Comme c’est le cas pour le modèle (14a), la seule statistique que nous pouvons calculer, est la matrice de variance covariance de la forme réduite X _t ._{Dans le cas multivarié, cette matrice s’écrit comme suit :}

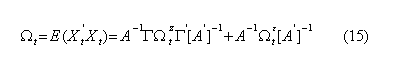
On note ici que dans la cas où le problème d’hétéroscédasticité ne se pose pas, le changement dans cette matrice de variance covariance est une indication pour le changement des paramètres du système. Toutefois, si les chocs sont hétéroscédastiques, ce changement dans la matrice de variances covariances serait non informatif sur la stabilité des paramètres.