1.4. Conditions d’existence de l’équilibre Tache solaire 

Afin de présenter la condition d’existence de cet équilibre tache solaire, Jeanne et Masson (2000) présentent une proposition caractérisant l’équilibre. D’après ces auteurs, l’équilibre tache solaire existe si et seulement si, il y a une multiplicité d’équilibres basés sur les fondamentaux (En d’autres termes la présence d’une multiplicité de solutions pour l’équation 7). Alors, si cette condition est satisfaite, il est possible de construire un équilibre tache solaire avec n’importe quel nombre de régime n ⁹¹ .

D’un coté, d’après cette condition, nous pouvons déduire que le nombre de régimes n’est pas le même que le nombre d’équilibres basés sur les fondamentaux. En fait, le nombre de régimes peut être arbitrairement large. Cela implique que les régimes sont arbitrairement très proches ou définis comme un continuum. Il en résulte ainsi qu’un régime peut être créé entre deux régimes déjà existants ⁹² .

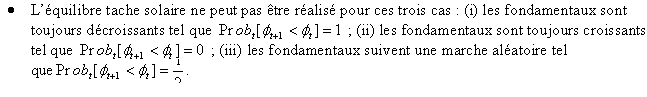
Ce corollaire présente trois cas pour lesquels le corollaire précèdent n’est pas vérifié et par conséquent l’équilibre tache solaire ne peut pas être réalisé. Les résultats de Krugman (1996) montrent bien la validité de ce corollaire du moins pour le premier cas où les fondamentaux sont toujours en dégradation. En effet, son modèle ne donne pas lieu à une multiplicité des équilibres quand les fondamentaux suivent une tendance déterministe de long terme. Il montre ainsi que si l’autorité est certaine d’une dévaluation à une date finie suite au mouvement des fondamentaux, la date effective de la dévaluation sera alors déterminée par un processus d’induction à rebours (backward induction). Dès lors, ce deuxième corollaire généralise le résultat de Krugman puisqu’il prend en compte deux autres cas radicalement différents : celui d’une amélioration des fondamentaux suivant un processus stochastique et celui d’une dynamique des fondamentaux selon une marche aléatoire.