Offre et demande d’investissement
Utilisons tout d’abord une fonction d’indifférence entre le rendement et le risque : soit la fonction agrégée de risque C associant à tout risque un rendement exigé.
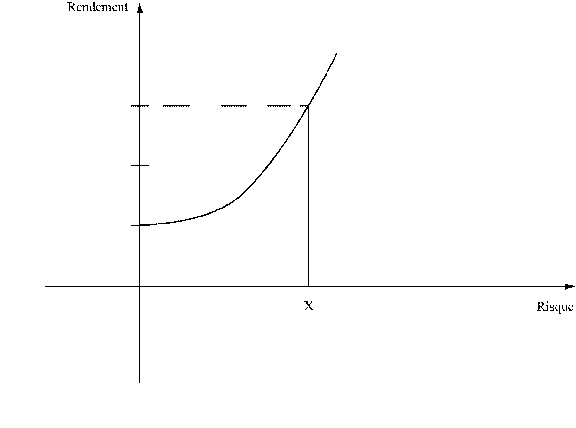
Au point X, il faudrait soit que le rendement soit multiplié par trois, soit que son prix soit divisé par trois. Par conséquent, tout investissement qui est à droite de la courbe d’indifférence doit voir son prix réduit ou son rendement augmenter.
Si nous admettons que les prix des biens d’investissement pour les PED sont des prix internationaux et donc absolument indépendants de la demande émanant de ces PED (et a fortiori des fonctions de risque spécifique de ces pays51), l’investissement X ne sera pas réalisé. On voit tout de suite que le risque joue un rôle essentiel dans l’investissement et donc dans la croissance des PED.
Plus généralement, l’existence d’un risque élevé au-delà duquel la courbe risque-rendement devient très pentue rend impossible, en tout cas à court terme, des ajustements par le prix. On a vu, au moment de la crise des Télécoms, des actifs se déprécier de 75 %, voire plus. Cette variation n’a pas un effet de rééquilibrage mais de déséquilibrage accru.
Peut-on dresser des fonctions d’offre et de demande de biens d’investissement ?
Dessinons une fonction associant équivalent certain et espérance.
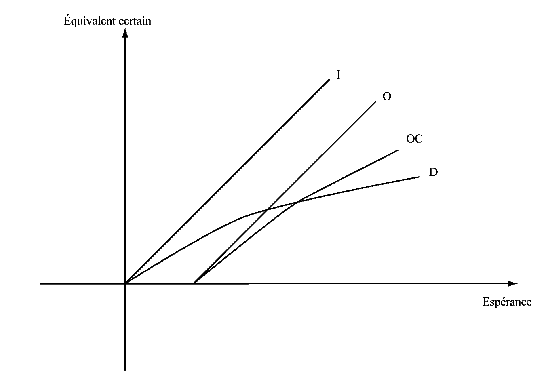
La courbe D associe (pour les investisseurs) à toute espérance de rendement un équivalent certain dont nous savons qu’il augmente relativement moins vite que l’espérance. Or l’équivalent certain est l’investissement. Nous avons donc une relation entre l’investissement réalisé et le rendement espéré, et la courbe D peut être assimilée à la courbe de demande d’investissement.
Supposons maintenant que les offreurs de biens d’investissement52, connaissant parfaitement le rendement espéré et sachant que les demandeurs le connaissent aussi, fixent un prix qui soit légèrement inférieur à l’espérance, et que leur offre soit parfaitement élastique : ils sont prêts à satisfaire toute demande qui serait faite à un prix acceptable. Nous aurons alors une fonction d’offre qui sera la droite O. Cette droite suit la diagonale EC=Espérance.
Nous pouvons aussi présumer que les offreurs, connaissant la fonction de demande, appliquent un prix inférieur lorsque l’espérance augmente (et que la demande faiblit). Nous aurons alors une fonction d’offre qui s’infléchit soit : OC.
On peut supposer également que les opportunités d’investissement auront tendance à se regrouper autour de la fonction de demande agrégée. On peut imaginer qu’à un instant donné il puisse exister une opportunité non détectée et dont le prix serait tel que le couple risque-rendement soit au-dessus de la courbe ; mais dès que les autres agents se seront rendu compte de cette opportunité, et pour peu que les marchés soient efficients, le prix augmentera de sorte que le couple risque-rendement sera proche de la courbe (de même si le couple est en dessous de la courbe).
On peut en déduire également le surplus pour l’offreur Y et le surplus pour l’investisseur X :
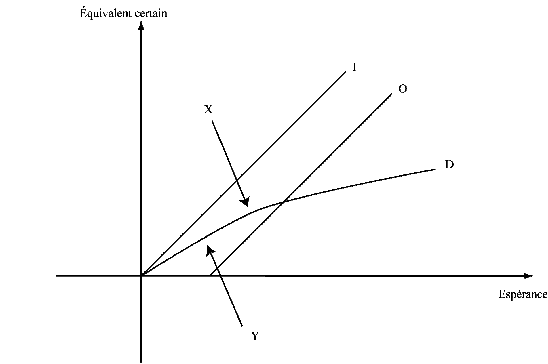
X est la différence entre le prix de l’investissement et l’espérance, c’est le bénéfice que l’investisseur réalisera en moyenne. Y est la différence entre ce que l’offreur était disposé à accepter et le prix effectif53.
La concentration des investissements autour de D (paragraphe précédent) justifie que l’on fasse l’amalgame entre la courbe de demande et la courbe des investissements effectifs.
Une place spéciale doit ici être réservée à l’aventurier. Le spéculateur a trouvé dans la littérature économique récente un certain réconfort : il contribuerait à équilibrer les marchés, à signaler aux autres agents les opportunités, à obliger les gouvernements incompétents à se corriger, etc. ; l’aventurier pour sa part n’est toujours pas sorti de son purgatoire : on le désigne avec mépris, parfois mêlé d’une certaine fascination. L’aventurier est pourtant essentiel au développement économique. Schumpeter avait fait de l’innovateur le moteur du dynamisme économique. Nous croyons que l’aventurier a un rôle plus large : l’innovateur innove dans des produits, des techniques, des marchés… l’aventurier conquiert des continents, il bouscule les convictions. Certes, il n’y a plus des Amériques à découvrir, mais on peut dans la vie d’aujourd’hui mettre un esprit d’aventure. L’étudiant qui montait des ordinateurs dans le garage de ses parents, celui qui importait en Angleterre des disques achetés en Belgique54, cet autre qui achetait des entreprises à l’encan ou enfin cet homme sans fortune qui s’était engagé à construire un palais en Arabie dans des délais records, tiennent plus de l’aventurier que de l’innovateur. Tous ces aventuriers se sont lancés dans leurs projets avec la conviction qu’une providence les ferait triompher de toutes les difficultés. Ayant réussi, ils ont montré que le niveau de risque objectif était plus bas qu’estimé et, par leurs succès et l’émulation, ils ont contribué à hausser le « courage » des autres agents55.
Revenons maintenant à notre spéculateur et reprenons le graphique 7. Imaginons deux demandes : le marché et un spéculateur. Le marché a une plus grande aversion au risque que le spéculateur (par définition) ; l’offre s’infléchit au point de rencontre avec la demande du marché et autorise le spéculateur à tirer parti de certaines opportunités dans la zone comprise entre sa courbe et celle de l’offre. Nous avons donc : la courbe S pour celle du spéculateur, Z pour la zone de spéculation, OC pour la courbe d’offre et D pour la courbe de demande.
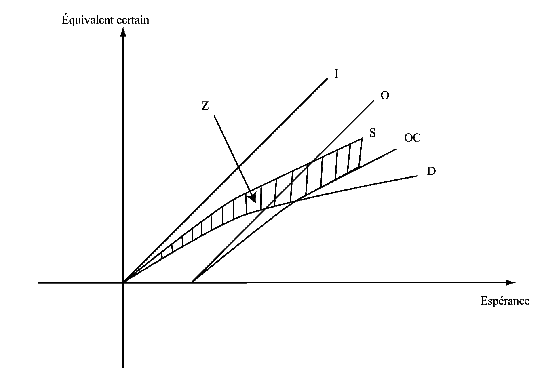
Dans le triangle désigné par Z, le spéculateur réalise un surprofit : il obtient un prix d’achat avantageux du bien d’investissement, et sa marge de profit est hors de proportion avec celle que réalisent les agents plus timorés. Évidemment ce sont des moyennes : on doit s’attendre à avoir des spéculateurs faisant de très gros profits et d’autres de très grosses pertes. Dans un pays où la prudence règne, les pertes décourageront l’initiative et les profits encourageront la médisance ; et dans celui qui valorise le risque et le succès, la réussite favorisera l’imitation et l’échec l’apprentissage.