3.3.2. La notion de champ conceptuel
Vergnaud (1981) considère qu’il n’est pas raisonnable d’étudier séparément l’acquisition de concepts (et de procédures) qui, dans les situations rencontrées et traitées par les élèves, sont difficilement dissociables. Il prend pour exemple l’aberration que pourrait présenter la juxtaposition d’études sur l’acquisition des concepts de multiplication et de division, de fraction, de rapport de nombre rationnel, de fonction linéaire, alors que l’enfant est confronté à des relations qui relèvent de l’ensemble de ces concepts, lorsqu’il doit résoudre des problèmes de type multiplicatif, en relation soit avec des proportions, des surfaces, des volumes.
Partant de là, il nomme champs conceptuels les regroupements de situations, de concepts et de représentations symboliques qu’il définit plus précisément comme des espaces de problèmes ou de situations-problèmes dont le traitement implique des concepts et des procédures de plusieurs types en étroite connexion (Vergnaud, 1981).
Vergnaud (1990) illustre la notion de champ conceptuel par deux exemples 63 : celui des structures additives et celui des structures multiplicatives 64 . La classification qu’il effectue en termes de types de problèmes à l’intérieur de chaque champ résulte en partie du constat que la même opération numérique peut permettre de résoudre des problèmes de difficultés très différentes.
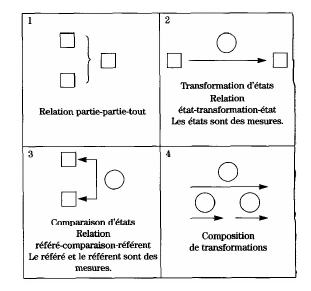
Vergnaud prolonge la réflexion sur l’enseignement en instrumentalisant sa théorie. Ainsi, afin de favoriser la compréhension des relations en jeu et de faire progresser les élèves dans le processus de conceptualisation, il propose que les élèves en difficulté dans la résolution de problèmes utilisent des diagrammes 65 , ces derniers pouvant être considérés comme des représentations isomorphes aux différentes structures de problèmes. Dès 1981, il introduit les types de diagrammes suivants, auxquels il attribue un statut transitoire : En tant que support pour les problèmes, ils sont faits pour être oubliés au fur et à mesure de la maîtrise de ces problèmes (Vergnaud et al., 1997, p. 34).