3.3.3. En prolongement de la théorie des champs conceptuels

Plusieurs recherches se sont intéressées aux effets provoqués par l’apprentissage de tels diagrammes sur les performances des élèves dans la résolution de problèmes. Levain (2000) a notamment expérimenté un protocole d’aide à la résolution de problèmes additifs et multiplicatifs auprès de 4 classes de CM1 et de CM2 basé sur un travail d’apprentissage et d’analyse de ces diagrammes correspondant aux structures de problèmes et intégrant (i) la présentation de diagrammes additifs et multiplicatifs, (ii) une mise en correspondance entre diagrammes et énoncés de problèmes, (iii) la construction d’énoncés de problèmes en fonction de diagrammes donnés. Levain a relevé après deux années d’expérimentation des effets positifs en CM2 sur la résolution des problèmes additifs entrant dans la catégorie composition de transformations. Il explique cette amélioration des performances par la condensation de l’information pertinente et la possibilité de contrôler les résultats en effectuant des essais ; il relève notamment l’effet facilitateur de la fixation d’un état initial hypothétique, par exemple la stratégie qui consiste à fixer 20 comme état initial (Figure 24). Toutefois, il précise bien que ces diagrammes ne traduisent qu’une modélisation de la situation parmi d’autres.

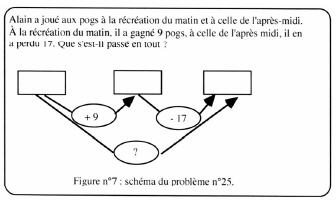
Il pointe aussi une amélioration des performances lors de la résolution de problèmes n’ayant pas fait l’objet d’un apprentissage spécifique. Les effets positifs d’ensemble avaient été moindres au cours de la première année d’expérimentation, avec cependant une amélioration des performances pour les problèmes considérés comme complexes ⁶⁶  : recherche d’une quatrième proportionnelle pour les problèmes multiplicatifs, et problèmes de composition de transformations pour les problèmes additifs.

Dans une autre étude conduite auprès d’élèves de SEGPA ⁶⁷ , Levain et al. (2006) confirment l’effet facilitateur provoqué par l’apprentissage et l’analyse de ces diagrammes. Il semble qu’une part de l’amélioration des performances puisse être attribuée au travail de discussion conduit par un adulte auprès de chaque petit groupe d’élèves en vue d’effectuer des analyses et des comparaisons des procédures utilisées, que ces dernières soient valides ou non.

Dans une étude conduite auprès d’élèves de CE2, Fischer (1993) avait montré d’une part qu’aucun élève ne sachant faire le diagramme correspondant à un des problèmes de l’expérimentation n’avait su résoudre le problème et que d’autre part tous les élèves qui avaient su le résoudre savaient aussi faire le diagramme, sans pour autant l’avoir effectivement dessiné. Cependant, l’étude ne permettait pas d’inférer que savoir réaliser un diagramme était une condition nécessaire pour résoudre le problème.

Julo (2002) manifeste un point de vue plus contrasté quant à ces diagrammes. Reconnaissant l’aide qu’ils apportent à la catégorisation, Julo voit toutefois un risque dans leur usage dans des situations d’apprentissage. Selon lui, les représentations symboliques conventionnelles ⁶⁸ choisies peuvent conduire à associer un schéma mental de problème à une forme symbolique spécifique. Julo regrette aussi le fait de privilégier l’explicitation de la structure des problèmes, alors que la diversité des formes d’organisation en mémoire est sans doute un atout majeur pour améliorer notre maîtrise d’un ensemble donné de problèmes. Il préconise plutôt l’usage d’une large base structurée de problèmes dans laquelle l’élève ferait des rapprochements et des différenciations, souvent implicites mais qui le conduiraient à une catégorisation sans exiger un passage par une explicitation de la structure des problèmes.

Notons que la théorie des champs conceptuels qui vise à expliciter les processus de conceptualisation s’étend à d’autres domaines que celui des mathématiques. Vergnaud cite l’électricité ⁶⁹ , la mécanique, les grandeurs spatiales, qui avec leurs spécificités respectives, impliquent une pluralité de situations et de concepts.

Compte tenu des travaux qu’il a effectués, Vergnaud nous paraît faire partie des précurseurs dans le domaine de la didactique des mathématiques, au même titre que Brousseau, Glaeser et Chevallard. Cependant, l’entrée psychologique qu’il a adoptée nous conduira à développer et à illustrer la théorie des champs conceptuels ainsi que les principes qui ont présidé à sa genèse dans le chapitre Psychologie de la présente partie.

Dans l’immédiat, nous nous tournerons vers des travaux en relation directe avec les théories citées dans ce volet de la didactique des mathématiques.