1.2.2. Analyse des performances en début de 6ème
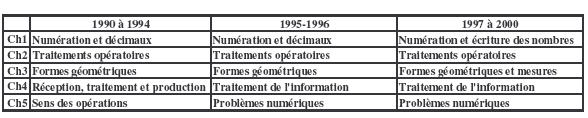
Dans le domaine des mathématiques, les compétences sont mesurées par des performances relatives à plusieurs champs. Depuis 1990, cinq champs des mathématiques qui revêtent des dénominations différentes (Tableau 11) suivant les années de passation sont évalués en début de 6ème : Ch1 : Numération ; Ch2 : Traitements opératoires ; Ch3 : Travaux géométriques ; Ch4 : Traitement de l’information ; Ch5 : Problèmes à données numériques. Les tableaux 12 et 13 présentent les différentes dénominations utilisées depuis 1990 par l’Institution scolaire.

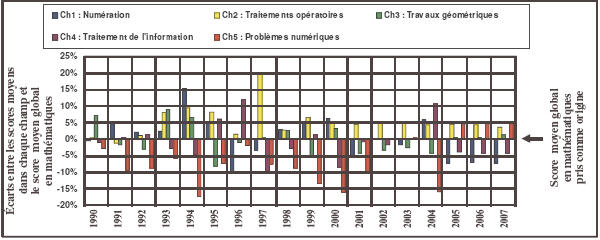
Les tableaux 14, 15, 16 présentent successivement les scores moyens obtenus par année, par champ et dans le domaine des mathématiques. Ces scores moyens sont, comme pour le CE2, des estimations des taux moyens d’items réussis par champ. Ceci rend comparables les résultats annuels, étant donné que dans chaque champ, le nombre d’items proposés varie d’une année à l’autre. Ces scores moyens sont rapportés à la base 100.
| 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | |
| Ch1 : Numération | 72,30 | 74,70 | 74,00 | 60,70 | 77,60 | 68,70 |
| Ch2 : Traitements opératoires | 73,30 | 68,90 | 73,00 | 66,30 | 71,80 | 71,50 |
| Ch3 : Travaux géométriques | 80,00 | 68,30 | 68,90 | 67,10 | 68,90 | 55,20 |
| Ch4 : Traitement de l'information | 71,80 | 70,40 | 73,20 | 55,50 | 57,60 | 69,50 |
| Ch5 : Problèmes numériques | 70,00 | 60,80 | 63,10 | 52,50 | 45,00 | 55,90 |
| Score Moyen Global en Mathématiques | 72,90 | 70,10 | 71,90 | 58,30 | 62,40 | 63,40 |
| 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | |
| Ch1 : Numération | 53,00 | 51,40 | 62,90 | 67,70 | 70,80 | 61,40 |
| Ch2 : Traitements opératoires | 64,30 | 74,50 | 62,80 | 69,60 | 70,00 | 71,30 |
| Ch3 : Travaux géométriques | 61,90 | 55,00 | 62,60 | 57,80 | 67,80 | 62,70 |
| Ch4 : Traitement de l'information | 74,80 | 45,00 | 57,20 | 64,30 | 56,20 | 66,00 |
| Ch5 : Problèmes numériques | 61,00 | 47,10 | 51,20 | 49,70 | 48,50 | 56,40 |
| Score Moyen Global en Mathématiques | 62,90 | 54,70 | 60,10 | 63,10 | 64,60 | 66,90 |
| 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | |
| Ch1 : Numération | 65,20 | 60,60 | 70,10 | 56,70 | 57,00 | 57,10 |
| Ch2 : Traitements opératoires | 69,90 | 67,20 | 68,60 | 68,30 | 68,30 | 67,90 |
| Ch3 : Travaux géométriques | 61,60 | 59,60 | 60,10 | 64,50 | 64,60 | 65,60 |
| Ch4 : Traitement de l'information | 63,30 | 62,10 | 75,00 | 60,10 | 59,80 | 60,00 |
| Ch5 : Problèmes numériques | 65,20 | 62,60 | 48,40 | 68,50 | 68,60 | 69,70 |
| Score Moyen Global en Mathématiques | 65,00 | 62,30 | 64,30 | 63,90 | 64,00 | 64,30 |
S’agissant des résultats aux évaluations de 6ème, les graphiques 6 et 7 révèlent, de 1994 à 2004, le même constat que pour les évaluations CE2 : les performances en résolution de problèmes pour les épreuves d’évaluation de 6ème sont systématiquement inférieures au score moyen global en mathématiques.
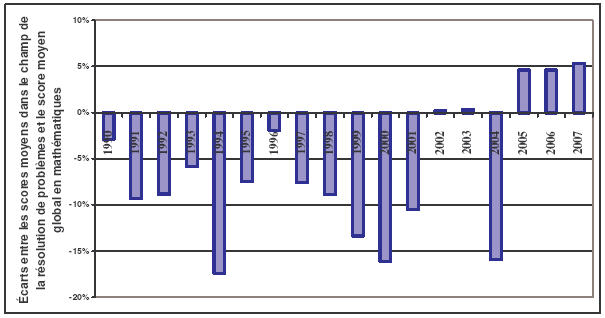
Pour le champ des problèmes à données numériques, plusieurs notes d’information publiées par le Ministère mentionnent des difficultés pour résoudre des exercices mettant en jeu des raisonnements complexes ou demandant la production d’une justification, l’interprétation de données présentes dans l’énoncé, l’organisation d’une démarche 115 .
Des difficultés relatives à la proportionnalité, à l’interprétation d’une division euclidienne sont également pointées certaines années. Rappelons que les contenus des épreuves ne sont pas constants d’une année sur l’autre et que, chaque année, un choix est opéré par les concepteurs des épreuves, quant aux compétences à évaluer.
L’étude conduite en 2001 par le Ministère de l’Éducation nationale (DEP, 2002) visant à comparer les performances avant et après les vacances scolaires d’été, montre que les écarts les plus importants entre la fin du CM2 et le début de la 6ème concernent tous les items qui évaluent les compétences en cours d’acquisition et qui mettent en jeu le sens de la division dans le cadre d’une situation-problème (46,4% de réussite en CM2 vs 39,7% en 6ème), la comparaison d’un produit donné avec un autre produit par calcul approché (40,4% de réussite en CM2 vs 33% en 6ème), l’analyse d’une situation numérique exigeant de prendre en compte plusieurs contraintes (54% de réussite en CM2 vs 44% en 6ème).
Cette même étude pointe l’absence d’écart significatif entre le CM2 et la 6ème à l’item évaluant la capacité à reconnaître une situation additive, cet item étant par ailleurs le mieux réussi de l’ensemble du champ. Nous nous interrogeons cependant sur les performances réalisées : 72,8% de réussite en CM2 vs 70,7% en 6ème puisque, selon cette étude, près de 3 élèves sur 10 ne seraient pas capables en début de collège de reconnaître une situation additive.
S’agissant des évaluations de septembre 2005, la synthèse établie par le Ministère de l’Éducation nationale 116 fait état, pour plus de sept élèves sur dix, d’une bonne maîtrise de la lecture et de l’interprétation des diagrammes. Les résultats révèlent aussi que deux élèves sur trois sont capables de résoudre un exercice 117 simple sur la proportionnalité directe, c’est-à-dire de reconnaître le type de situation et de mettre en jeu une technique faisant appel aux proportions linéaires.